zbadaj liczbę rozwiązań
rownanie: zbadaj liczbę rozwiązań równania w zależności od parametu m , |2x 1|= m−3
Jak to zrobic? Rysować to co po prawej i to co po lewej w jednym układzie współrzędnych i
później zobaczyć gdzie się przecinają i to będą rozwiązania? Proszę o pomoc!
2 lis 15:28
Kacper:
2 lis 15:30
rownanie: i tyle wystarczy? nie trzeba rozkładać tego na przypadki jakieś >0 i <0 ?
2 lis 15:38
rownanie: i jak potraktować to m−3 ? jako zwykłą prostą i postawiać normalnie pod m wartości i tam gdzie
się przetnie z wykresem z wartością bezwzględną to dla takiej wartości m wpisać : dla takiej
wartości m zachodzi równanie |2x 1|= m−3 ?
2 lis 15:40
rownanie: odpisze ktos?
2 lis 15:56
Eta:
Napisz porządnie lewą stronę równania ( bo na razie .........jest bez sensu)
2 lis 16:24
...:
− po pierwsze primo jak mówił pewien kabareciarz to zdecyduj się co masz pod tym modułem
|2x+1| czy |2x−1} a może |2x−1| czy wreszcie |2x+1| ...
− potem zrób wykres i "tnij" go stałą (pozioma) i ustalaj ilość rozwiązań.
Pamiętaj, że ta stała to nie m tylko m+3 a ustalić masz dla jakiego m
Takich i podobnych zadań było tu setki ... poszukaj ...
2 lis 16:31
rownanie: Przepraszam, zapomniałem o minusie |2x−1|=m−3
2 lis 16:31
...:
umiesz narysować wykres f(x)=|2
x−1|
?
2 lis 16:33
rownanie: tak , bez problemu , tylko nie wiem co dalej ,jak już go narysuję
2 lis 16:35
...:
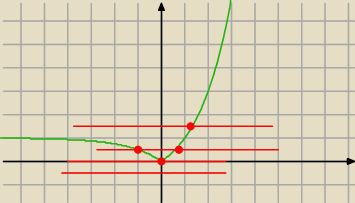
2 lis 16:37
rownanie: aaaaaaaaaaaaaa
już wszystko wiem, dziękuję bardzo za pomoc
2 lis 16:38
rownanie: a jakby to była prosta m+3 to nie ma znaczenia, prawda? zawsze przecinamy tam gdzie 1 , 2 i 0
rozwiązań, tak?
2 lis 16:40
...:
tak ... tam gdzie zmienia się ilość
ZAPISZ SWOJE ROZWIĄZANIE .. SPRAWDZIMY CZY SERIO ROZUMIESZ
2 lis 16:46
rownanie: 0 rozw dla m ∊(−∞,0)
1 rozw dla m=0 i m∊<1,∞)
2 rozw dla m∊(0,1)
2 lis 16:52
rownanie: Nie wiem ,czy dobrze
2 lis 17:04
rownanie: Jak będziesz mógł , to sprawdź, bo jestem ciekaw czy dobrze zrobiłem
2 lis 17:09
...:
oczywiście, że ..... NIE DOBRZE −:(
2 lis 17:11
...:
ta stała to nie m tylko m−3
Zatem 0 rozwiązań dla m−3<0 ⇒ m<3
itd
2 lis 17:13
rownanie: okej, to spróbuję porozpisywać dalej bo dałem dla stałej m
2 lis 17:13
rownanie: 0 rozw dla m<3
1 rozw dla m≥6
2 rozw dla m>3 (i tutaj nie wiem jaki znak , chyba lub bo suma, a więc: ) v m<6
a teraz jak ?
2 lis 17:33
b.: 0 rozw dla m<3 −− dobrze,
1 rozw dla m≥6 −− no taaak, też dobrze
2 rozw dla m>3 *i* (i powinno być, nie lub) m<6 −− ale to źle
2 lis 17:39