Ekstrema Funcji Pomocy
Pochodniak: Witam potrzebuje pomocy w 2 przykładach w jednym nie mam wogóle pomysłu jak zrobić natomiast w
drugim zamiast minimum wychodzi mi maximum w wyrkesie i niewiem gdzie popełniam błąd proszę
kogoś o rozwiązanie obu przykładów z góry bardzo dziękuje
a)x
4−6x
2+8x+1 Nie mam pojęcia jak je wykonać
| | x2−4 | |
b) |
| w tym wychodzi mi na wykresie maximum a nie minimum w 0 |
| | x2+4 | |
2 lis 12:08
ICSP: 1. Ustalasz dziedzinę
2. Liczysz pochodną
3. Rozwiązujesz równanie f'(x)
4. Masz dwie opcje :
− Liczysz drugą pochodną i sprawdzasz wartości f'(x0)
− Rysujesz wykres pierwszej pochodnej i z niego odczytujesz rozwiązania.
2 lis 12:12
Pochodniak: Wiem jak wyznaczać ekstrema tylko w tych 2 przykładach niewiem co robie źle w a)Niewiem jak
rozłożyc to bo pochdna wychodzi mi 4x3−12x+8
2 lis 12:18
Gracjan : a) f`(x)=4x
3−12x+8
Oblicz delte,miejsca zerowe, narysuj wykres. Dasz radę. Tutaj dziedzina to R.
| | 2x*(x2+4)−2x*(x2−4) | |
b)f´(x)= |
| |
| | (x2+4)2 | |
Tutaj też dziedzina to R. Rysuj wykres funkcji z licznika.
2 lis 12:19
Gracjan : W a użyj schematu Hornera
2 lis 12:20
ICSP: 4x3 − 12x + 8 = 0
x3 − 3x + 2 = 0
x3 − x − 2x + 2 = 0
x(x−1)(x+1) − 2(x−1) = 0
(x−1)(x2 + x − 2) = 0
(x−1)2(x+2) = 0
2 lis 12:21
Gracjan : Błąd w moim pierwszym poście, tam jest pocho dna do potęgi 3 więc użyj Hornera.
2 lis 12:21
Pochodniak: Gracjan i w b dochodze do wykresu i niewiem gdzie błąd że mam maximum w 0 a w odpowiedziach
jest minimum i niewiem gdzie błąd jest ...
2 lis 12:22
Gracjan : Ma być minimum w zerze. Funkcja z licznika jest rosnąca (16x) Prze chodzi przez zero'
pochylona' w prawo.
2 lis 12:26
Pochodniak:
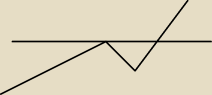
tam gdzie się odbija jest −4 a gdzie przechodzi mam 0
2 lis 12:28
Pochodniak: i z tego wykresy wychodziłoby na to ze w 0 powinno być maximum bo jest z plusa na minus
2 lis 12:29
Gracjan : Źle. Wymnoz jeszcze raz licznik i zredukuj wyrazy podobne. Ma być 16x w liczniku.
2 lis 12:30
Pochodniak: i wychodzi mi 16x
czyli razem powinno byc x(x+4)
2
2 lis 12:31
Gracjan : Powtórz materiał. W przypadku takiej funkcji wykres znaku pochodnej zależy TYLKO od znaku
licznika, bo mianownik jest zawsze dodatni. Rysujesz na wykresie tylko znak 16x.
2 lis 12:34
ICSP: x(x2 + 4)2
2 lis 12:36
Pochodniak: Gracjanie bardzo dziękuje za pomoc ISCP również
2 lis 12:38
Gracjan : Mam nadzieję, że już jasne
2 lis 12:39