geometria analityczna Marysia: Dany jest trójkąt ABC, w którym D=(−4,−1) ; E=(−1,−3) ; F=(3,2) są środkami boków odpowiednio AB, AC, BC. Wyznacz współrzędne wierzchołków tego trójkąta. po zrobieniu rysunku, wyobraziłam sobie okrąg wpisany w trójkąt, ale nie mam pojęcia jak rozkminić to zadanie. Proszę o rozjaśnienie mojego umysłu.

chica: Powinnas zaczac od tego ze wspolrzedne srodka odcinka sa srednia arytmetyczna wspolrzednych konca :3

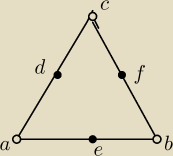
colki: Więc masz

⎧	ax+cx=−8
⎨	ax+bx=−2
⎩	bx+cx=6

⎧	ay+cy=−2
⎨	ay+by=−6
⎩	by+cy=4

Marysia: No i co dalej? wiem, że średnią arytmetyczną ale nie mam podanych współrzednych punktów ABC, a o to pytają w zadaniu.

	xA + XB
xs=		i tak samo z y, ale jak podstawie to nadal mam niewiadomą współrzędnych
	2

punktu a i b

Marysia: colki. skąd wzięty jest te wzór? rozumiem, że obliczana jest część wpólna tak?

Marysia: Nikt mi nie pomoże? jak zrobić to poprawnie? używając wzorów z działu geometria analityczna?

Marysia: Nikt mi nie pomoże? jak zrobić to poprawnie? używając wzorów z działu geometria analityczna?

colki: Wybacz juz już

colki: wiesz ze A(ax, ay), B(bx,by) C (cx, cy). Teraz piszemy z definicji sredniej arytmetycznej D[(ax+cx)/2, (ay+cy)/2] Resztę liczysz na tej samej zasadzie, mam tu na mysli punkty E i F. I powstają ci po pomnozeniu przez dwa trzy równania ze względu na x i trzy ze wzgledu na y<te co podałam wyzej>.

colki: Wiem że nie masz podanych punktów ale masz podany wynik czyli np −4=^ax+cx₂ Czy to jest jasne? Bo to wazne zebyś to zrozumiała

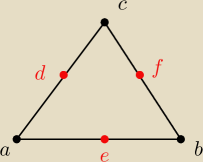
colki: A(a_x, a_y) B(b_x, b_y) C(c_x, c_y) D(−4, −1) −4=d_x −1=d_y →tak tez będę znaczyć wsp. punktów E i F E(−1, −3) F(3, 2)

⎧	dx=ax+cx2
⎨	ex=ax+bx2
⎩	fx=bx+cx2

⎧	dy=ay+cy2
⎨	ey=ay+by2
⎩	fy=by+cy2

Po podstawieniu:

⎧	−4=ax+cx2
⎨	−1=ax+bx2
⎩	3=bx+cx2

⎧	−1=ay+cy2
⎨	−3=ay+by2
⎩	2=by+cy2

Obustronnie mnożę każde równanie przed 2

⎧	−8=ax+cx
⎨	−2=ax+bx
⎩	6=bx+cx

⎧	−2=ay+cy
⎨	−6=ay+by
⎩	4=by+cy

Pozostaje ci rozwiązać układy równań i masz współrzędne wierzchołków