Nierownosc z wartoscia bezwzgledna kuba: |2x−3|<|x+2| help wiem ze to banal ale dla 3 os wyszedl 1 przypadek taki sam a 2 kazdemu inny dlatego tez pytam;S

kuba: help ktos

Kamil: będą 3 warunki przecież

Kamil: no tak tylko w 2 warunkach bedzie to samo obie f. liniowe dodatnie

Kamil: no tak tylko w 2 warunkach bedzie to samo obie f. liniowe dodatnie

ruda: |2x−3|−|x+2| <0

	1
{2x−3+x+2<0 ⇔ x<
	3

|2x−3|−|x+2|={−2x+3+x+2<0 ⇔x>5

	1
{−2x+3−x−2<0⇔ x>−
	3

Kamil: Obstawiam ze: x ∊ <−∞;¹₃> bo: 1) x < 5 2) x < ¹₃ 3) x < 5

Bogdan: Nie 3 warunki, poprawne jest stwierdzenie: należy rozpatrzeć nierówność w trzech

	3		3
przedziałach: (−∞, −2), <−2,		), <		, +∞)
	2		2

Kamil: nawiasy otwarte i znaki mi się pomyliły

Aza: rozpatrujesz przedziałami: 1/ x€( −∞, −2) 2/ x€<−2, ³₂) 3/ x€<³₂, ∞) dla 1/ −2x +3 < −x −2 => −x < −5 => x >5 −−−−sprzeczność w tym rozpatrywanym przedziale dla 2/ −2x +3 < x +2 => −3x <−1 +. x > ¹₃ cz. wspólna z danym przedziałem: x€(¹₃, ³₂) 3/ 2x −3 < x+2 => x <5 cz. wspólna. x€<³₂,5) odp: suma tych obydwu rozwiązań: to x€(¹₃, 5)

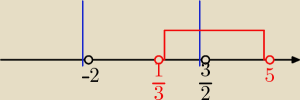
Bogdan: |2x − 3| < |x+2| Dla x∊(−∞, −2): −2x + 3 < −x − 2 ⇒ x > 5 sprzeczność,

	3		1
Dla x∊<−2,		): −2x + 3 < x + 2 ⇒ 3x > 1 ⇒ x >
	2		3

	3
Dla x∊<		, +∞): 2x − 3 < x + 2 ⇒ x < 5
	2

	1
Odp.: x∊(		, 5)
	3

AROB:

Aza:

kuba: no to jak mi wyszlo 1/3 i 5 to dobrze

kuba: a ma to sens jak robie |2x−3|<|x+2| 2x−3<x+2 2x−3>−x−2 i rozwiazuje? czy to jest niepoprawne?

kuba1: ?

kuba: powie ktos madry?

kubad: Bogdan prosze pomoz

Bogdan: Jeśli chodzi o Twoje pytanie dotyczące sensu, to taki sposób rozwiązywania, jaki przedstawiłeś w pytaniu, nie jest poprawny. Pokazałem wyżej, jak rozwiązuje się takie nierówności.