Udowodnij, że ania: W trójkącie prostokątnym ABC z wierzchołka kąta prostego poprowadzono wysokość CD. Udowodnij, że: |DB|/|DA| = |CB|² /|CA|² nie umiem tego mogę prosić o pomoc

daras: http://lmgtfy.com/?q=Udowodnij%2C+%C5%BCe%3A+%7CDB%7C%2F%7CDA%7C+%3D+%7CCB%7C2+%2F%7CCA%7C2+

ania: nie ma nigdzie tego −.−

ania: poza tym po to jest forum matematyczne by na nim pomagać mistrzu..

daras: to daj z siebie trochę pary leniwa istoto

ania: nie jestem leniwa tylko na rysunku sie skonczyło xd

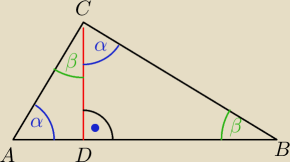
Mila: Mamy wykazać, że :

|DB|		|CB|2
	=
|DA|		|CA|2

ΔADC∼ΔACB cecha kkk⇔odpowiednie boki obu Δ są proporcjonalne.( wybieram przyprostokatne )

|CB|		|DC|
	=
|CA|		|DA|

ΔCDB∼ΔACB cecha kkk⇔odpowiednie boki obu Δ są proporcjonalne.

|CB|		|DB|
	=		mnożę stronami obydwie równości
|CA|		|DC|

|CB|		|CB|		|CD|		|BD|
	*		=		*		⇔
|CA|		|CA|		|AD|		|CD|

|CB|2		DB|
	=
|CA|2		|DA|

cnw

Eta: lub tak:

|DB|		|CB|
	=		⇒ |CB|2=|DB|*|AB|
|CB|		|AB|

|DA|		|CA|
	=		⇒ |CA|2=|DA|*|AB|
|CA|		|AB|

	|CB|2		|DB|
dzieląc stronami :		=
	|CA|2		|DA|

pigor: ..., ad. rozwiązania ... η , ja pamiętam twierdzenie czyli z tw. o kwadracie długości przyprostokątnej, który jest równy iloczynowi jej rzutu na przeciwprostokątną i długości tej przeciwprostokątnej. a więc do mojej "szuflady" leci tylko to: ponieważ : |CB|²=|DB|*|AB| i |CA|²=|DA|*|AB| /:stronami ⇒ |CB|²: |CA|²=|DB|: |DA| c.n.w.

Eta: Jasne π.. ( taki wzór jest nawet w karcie wzorów tylko o nim maturzyści zapominają

Mila: Zapominają też, że trzeba zauważyć podane rozwiązanie.

Kacper: A co oni pamiętają?