algebra kyrtap: Korzystając ze wzoru de Moivre’a obliczyć: (d*) (i − 2)²4 (13 + 9i)⁸

	(7 + i)11
(e*)
	(2 + i)22

W tych przypadkach każde wyrażenie mam na początku wyliczyć ze wzoru a następnie te wartości które wyjdą przemnożyć lub podzielić tak?

kyrtap: jak może ktoś potwierdzić iż mój plan działania będzie dobry proszę o komentarz

Mila: Nie będzie to takie proste , gdy od razu chcesz wzór . a) podpowiedź (−2+i)³=−2+11i [(−2+i)³]⁸*(13+9i)⁸= =[(−2+11i)*(13+9i)]⁸=(−125+125i)⁸=[5³*(−1+i)]⁸ to już proste dokończ, masz ładny argument, nie wykonuj potęgowania.

kyrtap: piękne dzięki w drugim też podobnie z tego co widzę

kyrtap: Myślisz Mila że na kolokwium materiał powinien nawiązywać do tego co przerabiamy na ćwiczeniach?

kyrtap: czekam na odpowiedź i chcę wrócić jeszcze na chwilę do zadania bo coś znalazłem ciekawego

Mila: To zależy od asystenta, musisz zapytać kolegów z wyższego roku. Czasem kolokwia są identyczne. Jeśli mieszkasz w akademiku, to nie problem zasięgnąć języka. Drugi przykład wymyśliłeś, czy mam też myśleć.?

kyrtap: Otóż znalazłem w swoich notatkach taką własność iż : Przy mnożeniu liczb zespolonych w postaci trygonometrycznej ich moduły się mnoży a argumenty(kąty dodaje) a przy dzieleniu moduły się dzieli a kąty odejmuje, tu chyba tą własność można zastosować

Mila: Oczywiście , ale argument trzeba mieć. Licz.

kyrtap:

	2
trudno wyliczyć bo sinβ =		a z tego nie mogę jednoznacznie powiedzieć ile wynosi β
	5

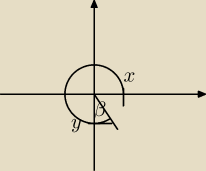
kyrtap: w sensie ja stosuję taką metodę iż wyznaczam w przypadku pierwszego wyrażenia Iz1I oraz sinα i

	π
cosα i potem staram się znaleźć ten kąt α = 3 *		+ β
	2

kyrtap: ajajajaj źle zrobiłem już wiem

kyrtap: w sumie nie wiem jak wyznaczyć tym sposobem argument tutaj

kyrtap:

	2√5
bo wyszło mi sinβ =
	5

bcd: No, wiesz... jak doliczysz sobie cosβ, to możesz doliczyć od razu tgβ i przedstawić β jako arctg. I podstawić...

kyrtap: za wiele mi to nie da

bcd: Póki ktoś nie powie, że masz zapisać wynik w postaci algebraicznej, to daje Ci to nic innego jak... poprawny wynik. A więc na kolokwium bardzo dużo.

kyrtap: Algebra sama mówi za siebie

bcd: Nie wiem tylko, co można zrobić ze złożeniem funkcji typu: cos(arctg+arctgβ+2kπ) −> takie właśnie występowałyby w odpowiedzi.

Mila: To tak:

	7+i		1
(		)11*(		)11=
	2+i		2+i

	(7+i)*(2−i)		2−i
=(		)11*(		)11
	5		5

licz dalej sam , wyjdzie w końcu ładny argument.

Mila: Czekam na wynik

kyrtap: w przypadku Mili rozwiązania w jej ostatnim zapisie [5³*(−1+i)]⁸ co należy potem zrobić aby skorzystać ze wzoru bo nie kumam

kyrtap: ok jak mi jeszcze dasz maleńką podpowiedź

kyrtap: sory już wiem jeju wszystko mi się miesza

kyrtap: zaraz podam wynik

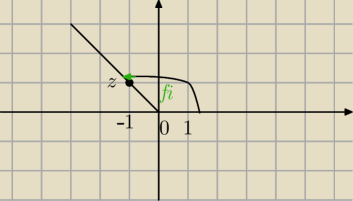
Mila: Jak to nie wiesz? 5²⁴*(−1+i)⁸ z=(−1+i) |z|=√2

	−1		−√2
cosφ=		=−
	√2		2

	1		√2
sinφ=		=
	√2		2

	3π
φ=		można od razu graficznie ustalić
	4

	3π		3π
524*z8=524*(√2)8*( cos(8*		)+i sin(8*		) )
	4		4

kończ

kyrtap: wyszło mi w pierwszym podpunkcie 16 * (−5³)⁸

kyrtap: czasami moje rozkojarzenia musisz wybaczyć mi

Mila: Skąd ten minus? 5²⁴*16

Mila: Drugie licz , bo zaraz ide spac.

kyrtap: ok już szybciutko liczę

kyrtap: 32 − 32i?

Mila: cd.

	15−5i		2−i
(		)11*(		)11=
	5		5

	5*(3−i)		2−i
=[		*		]11=(1−i)11
	5		5

z=1−i punkt (1,−1)

	π
φ=2π−
	4

|z|=√2

	7π		7π
z11=√211*(cos(11*		)+isin(11*		)
	4		4

.. z¹¹=−32−32i

Mila: Dobranoc

kyrtap: Mila na pewno we wzorach redukcyjnych się nie pomyliłaś

kyrtap: dobra ja źle zrobiłem dzięki Mila i dobranoc

kyrtap: Mila jak możesz spr swój wynik bo ten − przed 32 mi się nie zgadza

Gray: Spostrzegawczość @Mili zasługuje na najwyższe uznanie Jak zwykle z resztą. Z zadaniami w których mamy podnieść liczbę zespoloną do potęgi i mamy skorzystać ze wzoru de Moivre'a możemy poradzić sobie i w taki sposób jak pokażę na przykładzie poniżej. Nie wymaga on znajomości argumentu liczby zespolonej, którą potęgujemy. Przykład. (13+ 9i)⁴ = ? z= 13+ 9i ⇒ |z| = √169 + 81 = √250

	13
cosα=
	√250

	9
sinα =
	√250

α = ? nie potrafimy wyznaczyć α. Trudno. Idziemy dalej: (13+ 9i)⁴ = (|z| (cos α + isinα))⁴ =( √250 )⁴ (cos4α + i sin 4α) =..... ________________________________________________ (cosa + i sina)⁴ = ... wzór dwumianowy Newtona... = cos⁴a + 4cos³a i sina − 6cos²asin²a − i 4 cosa sin³a + sin⁴a oraz (cosa + isina)⁴ = cos4a + isin4a. Porównując części rzeczywiste i urojone mamy: cos4a = cos⁴a − 6cos²asin²a + sin⁴a sin4a=4cos³a sina − 4 cosa sin³a ____________________________________ .....= 250² ( cos⁴α − 6cos²αsin²α + sin⁴α + i(4cos³α sinα − 4 cosα sin³α) )=... Aby dokończyć wystarczy w powyższym wzorze podstawić

	13
cosα=
	√250

	9
sinα =
	√250