zadania optymalizacyjne nick: Suma długości dwóch boków trójkąta wynosi 12 cm a miara kąta pomiędzy tymi bokami jest równa 120 stopni . Oblicz jaką najmniejszą wartość może mieć obwód tego trójkąta. proszę o pomoc. niby wiem że z tw. cosinusów ale coś nie wychodzi..

Jolanta: a ak to robisz ?

Jolanta: jesteś ?

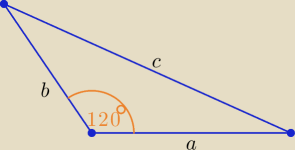
Eta: a+b=12 ⇒ a= 12−b , b∊(0,12) z tw. kosinusów

	1
c2=a2+b2−2ab*cos120o , cos120o= −cos60o= −
	2

c²= a²+b²+ab ⇒ c²= (a+b)²−ab = 144−ab= 144−(12−b)*b= b²−12b+144 L=a+b+c ⇒ L(b)= 12+√b²−12b+144 −−−osiąga minimum wtedy, gdy:

	12
b2−12b+144 −−− osiąga minimum ⇒ bmin=		=6
	2

zatem c_min=c(6)=√36−72+144= 6√3 L_min= 12+6√3= 6(2+√3) [j]

nick: dziekuję bardzo za pomoc, już znalazłam moje błędy rachunkowe do momentu L(b)=.... Tylko nie rozumiem końcówki skąd osiąga minimum?

Jolanta: narysuj parabolę jeżeli a>0 to minimum ma dla x_w

Jolanta:

	−b
xw=
	2a

nick: ahaa no tak. już wiem. dzięki

Eta: