funkcja MaćOK: Funkcja f jest określona wzorem f(x) = |x−1| − x − m dla wszystkich liczb rzeczywistych x. Wyznacz wszystkie wartosci parametru m, dla których funkcja ma tylko jedno miejsce zerowe.

kyrtap:

	⎧	x − 1 − x − m gdy x − 1 ≥0
f(x) =	⎨
	⎩	−x + 1 − x − m gdy x−1 <0

pigor: ..., otóż dana funkcja f(x)=|x−1|−x−m ma 1 miejsce zerowe, czyli równanie f(x)=0 ma dokładnie 1 pierwiastek ⇔ |x−1|−x−m=0 ⇔ |x−1|=x+m i m >−1 ⇔ m∊(−1;+∞) .

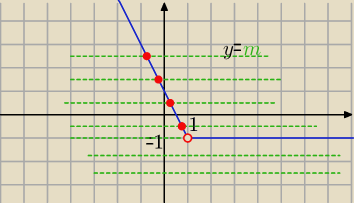
Eta: f(x)=0 ⇒ |x−1| −x= m g(x)= |x−1|−x , h(x)=m { −1 dla x≥1 g(x)= {−2x+1 dla x<1 y=m f(x) ma jedno miejsce zerowe dla m∊(−1,∞)