Geometria duduś: Przez środek S okręgu wpisanego w trójkąt ABC i wierzchołek C tego trójkąta poprowadzono prostą CS. Przecina ona okrąg opisany na trójkącie ABC w punkcie K. Wykaż, że |KA| = |KS|

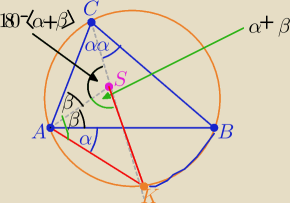
Eta: S −−− środek okręgu wpisanego w trójkąt ABC i jest punktem przecięcia dwusiecznych kątów wewnętrznych trójkątaABC to prosta CS jest dwusieczną kąta przy wierzchołku C prosta AS jest dwusieczną kąta przy wierzchołku A zatem |<ASC|= 180^o−(α+β) ⇒|<ASK|= α+β Z treści zad. punkt K leży na okręgu opisanym na trójkącie ABC Kąty wpisane w ten okrąg i oparte na tym samym łuku mają równe miary zatem : |<KAB|=|<KCB|= α więc |<KAS|= α+β =|<ASK| ⇒ że trójkąt ASK jest równoramienny o ramionach |KA|= |KS| c.n.u

Odkop xd: Okrąg wpisany w trójkąt a nie opisany sory że odkopuje ale nie kapuje tego zadania

Eta: Czego tu nie rozumiesz? Czytaj ze zrozumieniem ! Nie rysowałam okręgu wpisanego ..... tylko zaznaczyłam jego środek S jako punkt przecięcia dwusiecznych kątów trójkąta Okrąg "duży" −−− okrąg opisany na trójkącie Wszystko dokładnie opisałam Drugi raz nie chce mi się pisać tego samego