Do sprawdzenia - określ wzajemne położenie prostej i okręgu, jeśli: alysanne: Do sprawdzenia − określ wzajemne położenie prostej i okręgu, jeśli: l: 2x + y + 1 = 0 o: x² + y² − 2x + 6y = 0 A = 2, B = 1, C = 1 o: x² + y² − 2x + 6y = 0 x² − 2x + y² + 6y = 0 (x−1)² + (y+3)² = 10 r = √10 S(1,−3) d(S,l) = I 2 − 3 + 1I/√4 + 1 = 0 d(S,l) ≠ r = √10, a więc prosta l nie jest styczna z okręgiem

Janek191: Prosta przechodzi przez punkt S , czyli ma dwa punkty wspólne z okręgiem ( inaczej mówiąc − przecina okrąg )

alysanne: Gdzie w takim razie popełniłam błąd? Bardzo proszę o pomoc

Janek191: Nigdzie − odległość prostej od S = ( 1 ; − 3) wyszła 0 , czyli prosta przechodzi przez S i dlatego przecina okrąg Nie jest styczna do okręgu. Gdyby d wyszło √10 , to prosta byłaby styczna do okręgu .

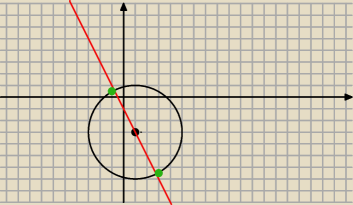
5-latek: Nigdzie nie popelnilas bledu nalezy tylko wiedziedz ze prosta ma z okregiem dwa punkty wspolne tak jak tutaj jeden punkt wspolny i nie ma z nim zadnych punktow wspolnych

alysanne: Aha, już rozumiem. W takim razie dziękuję