Bardzo proszę o pomoc w wyznaczaniu dziedziny :( bum: Wyznaczyć dziedzinę funkcji: f(x)= √2x²−5x−3 x³+x²−x−1 Całe to wyrażenie jest pod pierwiastkiem, nie wiedzialam jak to tutaj zaznaczyć Aha, i tam jest dzielenie, czyli 2x²−5x−3 dzielone przez x³+x²−x−1

magda: to całe wyrażnie pod pierwiastkiem ≥0 z założeniem że wyrażenie z mianownika ≠0

bum: Ale tam w mianowniku rozłożyć to na czynniki i te "x" które wyjdą mają być ≥ 0?

bum: A ktoś, cos oprócz tego?

Martiminiano: Nie. x∊(−∞ ; −¹₂> ∪ <3 ; +∞) \ {−1}

bum: Ojeeej. A skąd Ci takie coś wyszło?

Martiminiano: To licznik i mianownik jest pod pierwiastkiem, czy tylko licznik?

bum: I to i to

Martiminiano: To co napisałeś/aś jest równoważne z pierwiastkiem z licznika razy 1/pierwiastek z mianownika. Pierwiastek z licznika możliwy dla x∊(−∞ ; −¹₂> ∪ <3 ; +∞).

	1
W drugim przypadku		mianownik >0
	√x3+x2−x−1

(x+1)²(x−1)>0 Pierwszy nawias x∊R\{−1}, więc pozostaje nam rozpatrzyć 2. x−1>0⇔ x>1 Rozwiązaniem wszystkiego jest suma rozwiązań z (−∞ ; −¹₂> ∪ <3 ; +∞) i tego drugiego.

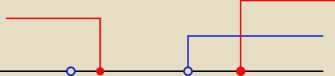
Martiminiano: Pusta niebieska kropka to −1, pierwsza czerwona −0.5, druga pusta niebieska to 1, druga czerwona to 3.

Martiminiano: Trochę to wszystko zagmatwałem, w razie czego pytaj. Po prostu w liczniku masz do rozwiązania przypadek 2x²−5x−3≥0, a w mianowniku x³+x²−x−1>0, a rozwiązaniem całości jest suma tych pojedynczych rozwiązań.

bum: Suuuper, wszystko już rozumiem, dzięki Ci bardzo!