Funkcja wykładnicza Maciej: Zbadaj liczbę rozwiązań równania w zależności od wartości parametru m m∊R |2−(¹₃)^x|=m²−1 Jak to się robi?

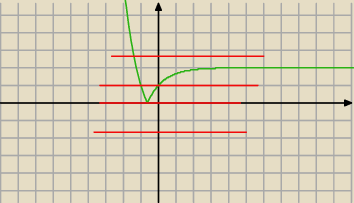
===: pamiętaj, że te czerwone stałe to m²−1

Maciej: dziękuję ale mógłbym prosić o przekształcenia? bo chciałbym to zrozumieć..jak się po kolei przesuwa itd..

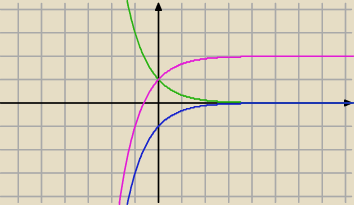
===: ...zielony (1/3)^x ... niebieski −(1/3)^x ... fiolet −(1/3)^x+2

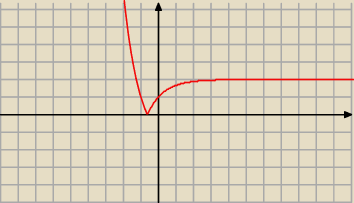
===: czerwony .... |−(1/3)^x+2|

Maciej: Wydaje mi się, że będzie y=3^x −−−Soy−−−>y=(¹₃)^x y=(¹₃)^x −−−Sox−−−−>y=−(¹₃)^x y=−(¹₃)^x−−−−Tu[0,2]−−−>y=2−(¹₃)^x y=2−(¹₃)^x−−−−−zach y≥0, Sox y<0 y=|2−(¹₃)^x|

Maciej: czy tak? i dziękuję za obrazki

Maciej: ?

Maciej: halo?

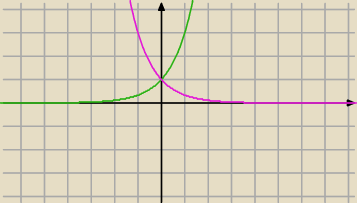
===: ... może jeszcze przez Poznań − Chyba wiesz jak wygląda f(x)=(1/3)^x i to jest funkcja podstawowa (ale bawić się możesz) 3^x .... zielona 3^−x ... fiolet

Maciej: Hmm no tak..ale ja niezbyt rozumiem m²−1 ... skąd ja mam wiedzieć gdzie to się na wykresie zaznacza? w Odpowiedzi mam: równanie nie ma rozwiązań dla m∊(−1,1); ma jedno rozwiązanie dla m∊(−∞,−√3>U{−1,1}U<√3,+∞); dwa rozwiązania dla m∊(−√3,−1)U(1,√3) jak to stąd odczytać?

===: ... tu cię boli −

===: ... pisałem o 21:57 że ta czerwona stała to to m²−1 Jak widzisz jeśli jest ona mniejsza o 0 ....to brak rozwiązań czyli dla m²−1<0 0 rozwiązań a kiedy m²−1<0 ? (m−1)(m+1)<0 ⇒ m∊(−1,1) itd