 1. W trójkącie równoramiennym podstawa ma długość 2a, a wysokość poprowadzona do tej podstawy
ma długość h. W trójkąt ten wpisano okrąg, a następnie poprowadzono styczną do okręgu,
równoległą do podstawy trójkąta. Oblicz długość promienia okręgu i długość odcinka stycznej
zawartego w trójkącie.
2. W trójkącie ABCD połączono środek M ramienia z końcami ramienia CD. Wykaż, że pole trójkąta
CMD jest równe połowie pola trapezu.
3. Obwód trójkąta prostokątnego jest równy 60 cm, a wysokość poprowadzona do
przeciwprostokątnej ma długość 12 cm. Oblicz długości boków tego trójkąta.
1. W trójkącie równoramiennym podstawa ma długość 2a, a wysokość poprowadzona do tej podstawy
ma długość h. W trójkąt ten wpisano okrąg, a następnie poprowadzono styczną do okręgu,
równoległą do podstawy trójkąta. Oblicz długość promienia okręgu i długość odcinka stycznej
zawartego w trójkącie.
2. W trójkącie ABCD połączono środek M ramienia z końcami ramienia CD. Wykaż, że pole trójkąta
CMD jest równe połowie pola trapezu.
3. Obwód trójkąta prostokątnego jest równy 60 cm, a wysokość poprowadzona do
przeciwprostokątnej ma długość 12 cm. Oblicz długości boków tego trójkąta.
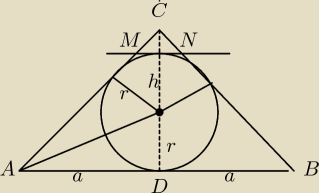
| 2P | 2P | |||
r= | 2a,b,c − boki Δ, b=c r= | |||
| 2a+b+c | 2a+2b |
| 2*1/2h*2a | h*a | |||
r= | = | b wylicz z Δprostokątnego ADC b=√a2+h2
| ||
| 2a+2b | a+b |
| h*a | ||
r= | ||
| a+√a2+h2 |
| 2a | h | ||
= | |||
| MN | h−2r |

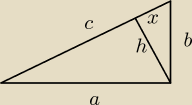 zad 3
60=a+b+c
b2=122+x2
c2=a2+b2
122+(c−x)2=a2
wszystko ma być spełnopne razem − powodzenia w liczeniu
zad 3
60=a+b+c
b2=122+x2
c2=a2+b2
122+(c−x)2=a2
wszystko ma być spełnopne razem − powodzenia w liczeniu
