PARAMETRY Stte: Wyznacz te wartości paramertu m(m∊R) dla których oba rozwiązania równania x²−2mx+m²−1=0 są większe od −2 i mniejsze od 4. Więc ... co tu trzeba zrobić po kolei> najpier załozenie ze Δ≥0 , następne to pewnie 4>x₁>−2 i 4>x₂>−2 ALE CO DALEJ?

Matematyk: x₁=−b+√b²−4ac*¹_2a x₂=−b−√b²−4ac*¹_2a Gdzie b=−2m a=1 c=m²−1

Stte: Heh tyle to ja umiem wiem jak sie oblicza delte i te sprawy tylko jak wyliczyc te wartosci wieksze od −2 a mniejsze od 4?

Nikka: nie wiem czy dobrze myślę, ale obliczyłabym deltę a następnie oba pierwiastki w zależności od parametru m, następnie rozwiązała nierówności, które zapisałaś dla obu pierwiastków (podstawiając pod x₁ i x₂ to co wyjdzie), otrzymasz jakiś przedział/y (m∊...) i na koniec część wspólna wszystkich warunków, które ma spełniać m (czyli z założenia o delcie i tego wyjdzie co z rozwiązania nierówności)

Matematyk: Może i umiesz, ale kiepsko z użyciem w praktyce Δ=4m²−4(m²−1)=4m²−4m²+4=4 √Δ=2 x₁=(2m+2)*¹₂ x₁=m+1 x₂=(2m−2)*¹₂ x₂=m−1 4>m+1>−2 3>m>−3−Z_a 4>m−1>−2 5>m>−1−Z_b Z_a ∪ Z_b=(−1;3)−tylko tych nawiasów nie jestem pewien, który obrazuje−to jest, a który ta wartość nie należy.

Bogdan: f(x) = x² − 2mx + m² − 1 Oba rozwiązania równania x² − 2mx + m² − 1 = 0 są większe od −2 i mniejsze od 4. a = 1, b = −2m, c = m² − 1,

	−b		2m
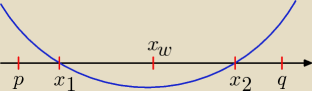
p = −2, q − 4, x1∊(−2, 4) i x2∊(−2, 4), xw =		=		= m.
	2a		2

Założenia: 1. a ≠ 0 2. Δ > 0 3. a*f(p) > 0 4. a*f(q) > 0 5. x_w > p 6. x_w < q. Rozwiązaniem zadania jest przedział wspólny rozwiązań podanych sześciu nierówności.