funkcja kwadratowa Majk: Podaj wszystkie wartości parametru m, dla których równanie |x² − 6x + 5| + m − 2 = 0 ma dokładnie 2 dodatnie rozwiązania. Robię to w ten sposób: rozbijam to równanie na 2 równania: 1) x² − 6x + 5 + m − 2 = 0 oraz 2) −x² + 6x − 5 + m − 2 = 0 W obu równaniach robię 3 warunki: 1) Δ > 0 żeby były 2 rozwiązania 2) x1x2 > 0 i 3) x1 + x2 > 0 bo pierwiastki mają być dodatnie W pierwszym równaniu częścią wspólną tych trzech warunków jest m∊ (−3, 6) a w drugim równaniu m∊ (−2, 7). Wynik z tyłu książki to jednak m∊ (−3, −2) ∪ {2}. Co robię źle?

===: rozbicie jak to określasz na dwa równania jest NIEPOROZUMIENIEM

Lukas: |x²−6x+5|+2 Narysować f(x)=x²−6x+5 odbić to co pod osią ox i przesunąć całość o dwie jednostki do góry

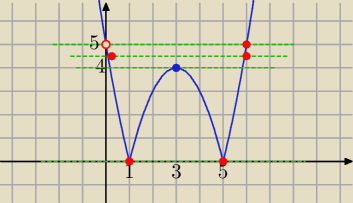Eta: f(x)= |x²−6x+5| y=k , k= 2−m równanie ma 2 dodatnie rozwiązania dla k=0 ⇒ 2−m=0 ⇒m=2 lub dla k>4 i m<5 ⇒ 2−m>4 i 2−m<5 ⇒ m∊(−3.−2)

Majk: Dlaczego rozbicie na 2 równania jest nieporozumieniem? Wytłumaczcie bo nie wiem czemu mam tak nie robić.

===: ... możesz ... jeśli określisz przedziały !

Majk: W sensie? Nie rozumiem

===: |x²−6x+5| wyrażenie pod modułem może przyjmować wartości ujemne, dodatnie bądź równe 0) określasz przedziały gdzie jest <0 a gdzie ≥0 ... i dla takich założeń rozpisujesz