liczby tyu: cześć. Mam takie zadanie Sprowadź dane wyrażenie do najprostszej postaci wiedząc, że x ∊ (1;3) Ix−8I Wiem jak to zrobić, bo pokazany jest na yt podobny przykład, ale nie wiem dlaczego tak to trzeba zrobić. W necie to jest wytłumaczone w ten sposób Zanim opuścisz wartość bezwzględną, musisz rozstrzygnąć czy wyrażenie pod wartością bezwzględną jest nieujemne czy ujemne. W drugim wypadku, opuszczając wartość bezwzględną, musisz zmienić znak. 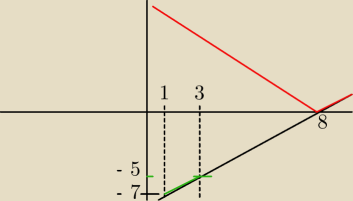Z wykresu wynika, że f=x−8 dla x ∊ (1;3) ma wartości (−7;−5), czyli ujemne. Ale co z tego wynika

daras: a jakie jest TO wyrażenie

tyu: Ix−8I

Metis:

Eta: |x−8| = −( x−8)=−x+8 dla x∊(1,3)

tyu: Dzięki wszystkim, ale nadal nie rozumiem.

Metis: Mi nie musisz dziękować

razor: |x−8| = x−8 dla x ∊ <8, +∞) |x−8| = −x+8 dla x ∊ (−∞, 8) przedział (1,3) należy do przedziału (−∞, 8), więc dla x ∊ (1,3): |x−8| = −x+8

tyu: wreszcie razor zrozumiałem Dziękuję

daras: ale ja nadal nie rozumiem o co pytałeś