Nierówność wykładnicza K: witam, proszę o pomoc w rozwiązaniu tej nierówności krok po kroku z góry dziękuję ! 6¹+x + 6¹−x ≤ 37 Doszłam do momentu, gdy: 6^x * 6¹ + 6¹/6^x ≤ 6⁶ + 6⁰ czy poprawnie wykonałam to działanie ? co dalej ?

K: w sumie niepotrzebnie rozbijałam chyba to 37, równanie według mnie powinno wyglądać tak: 6^x * 6 + 6/6^x ≤ 37 ⇒ 6^x = k 6k + 6/k ≤ 37/*k 6k² + 6 ≤ 37k 6k² + 6 − 37k ≤ 0 no ale delta wychodzi z kosmosu... już nie wiem co robić.

PW:

	6
6·6x +		≤ 62+ 1
	6x

PW: Dobrze, nie trzeba tej sztuczki z 37, a delta jest cacy.

K: Faktycznie, już za długo nad tym siedzę i się miesza... Dziękuję

K: Ok, k₁ = 1/6 i k₂ = 6, co później z tym robię ?

K: aaa ok, przyrównuję sobie k₁ = 6^x i k₂ = 6^x, co mi daje, x = −1 i x = 1, co dalej ?

PW: Jeszcze za wcześnie na iksy, była nierówność dla k, k>0: 6k² − 37k + 6 ≤ 0. Obliczyłas miejsca zerowe funkcji kwadratowej po lewej stronie − rysujesz parabolę i wyciągasz wnioski − jakie musi być k. Dopiero potem przechodzisz od nierówności dla k do nierówności dla 6^x i w konsekwencja dla x.

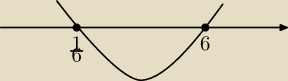
K: ok no to będzie wyglądać tak mniej więcej dla k.

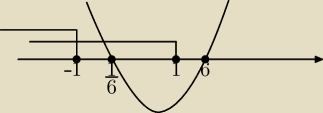
K: iksy będą równe: x = −1 i x = 1 teraz to ma wyglądać tak ?

K: po prostu nie pasuje mi to wszystko do rowiązania które ma się zawierać w {−1,1} według mojej odpowiedzi. zgłupiałam.

Kacper: Jak można zgłupieć?

K: według mnie odpowiedzią powinno być {1/6 i 1}...