Określ liczbę rozwiązań olciuszek: Określ liczbę rozwiązań podanego równania w zależności od parametru m. a) x³ + (1−m²)x − m=0 b) x³ + (1−m)x² − m²=0

===: studia?

olciuszek: Nie, 2 liceum

===: ... ciekawe zadanka −

ICSP: Wskazówka do a) : Zauważ, ze x = m jet pierwiastkiem

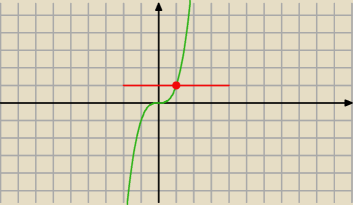
===: b) x²(x+1−m)=m² Wiemy, że pierwiastkiem podwójnym dla f(x)=x²(x+1−m) jest x₁=0 Znak pierwiastka g(x)=x+1−m x₂>0 dla 1−m<0 czyli dla m>1 x₂<0 dla 1−m>0 czyli dla m<1 x₂=x₁ dla m=1 Teraz rozpatrujesz: dla m=1 masz x³=m² i jeden pierwiastek

olciuszek: x3 + (1−m2)x − m=0 (x² + mx +1)(x−m)=0 Δ= m²− 4(1*1) Δ= m²−4 Dla Δ>0 m²−4>0 m∊(−∞;−2 ∪2;+∞) 3 rozwiązania Dla Δ=0 m²−4>0 m= 2⋀ m=−2 2 rozwiązania Dla Δ<0 m²−4>0 m∊(−2:2) − 1 rozwiązanie Dla m= 1 lub −1 1 rozwiązanie Tak?

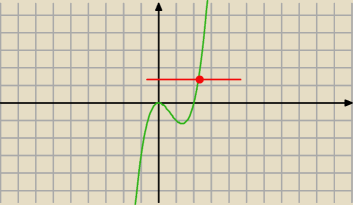
===: dla m>1 x₂>0 pierwiastek ten jest na prawo od x₁=0 Wykres może wyglądać tak "Tniemy" go stała m² (pamiętamy, że w tym przedziale m>0) Jeden pierwiastek

ICSP: Wynik poprawny, ale rozwiązaniu brakuje rozpatrzenia przypadku gdy m jest pierwiastkiem funkcji kwadratowej. Oczywiście widać, ze to nie zajdzie, ale należy zwrócić na ten fakt uwagę

ICSP: Już nie mówię o kopiowaniu nierówności m² − 4 > 0

olciuszek: No tak Dzięki