funkcje zadanie: Zbadac istnienie granic (x→0 i y→0)

	xy2
1) lim
	x2+y4

Niech y²=a (x→0 i a→0)

	xa
lim
	x2+a2

niech x=rcosα oraz a=rsinα (r→0⁺)

	rcosαrsinα
lim		=lim cosαsinα granica nie istnieje (zalezy od α)
	r2cos2α+r2sin2α

2) (x→2 i y→0)

	sin(xy2)
lim
	y2+(x−2)2

(w granicy jest od lewej x→2 potem y→0; w drugiej linijce na odwrot)

	sin(xy2)		1		1
lim (lim		)=lim		=		=∞
	y2+(x−2)2		(x−2)2		0

	sin(xy2)		sin2y2		sin2y2
lim (lim		)=lim		=2*lim		=2*1=2
	y2+(x−2)2		y2		2y2

granice iterowane sa rozne wiec granica funkcji wyjsciowej nie istnieje 3) (x→0 i y→0)

	sin(x4+y4)
lim
	x2+y2

	sin(x4+y4)		|sin(x4+y4)|		|(x4+y4)|
0≤|		|=		≤		≤
	x2+y2		x2+y2		x2+y2

|x|4+|y|4		x2		y2
	=x2		+y2		=(x2+y2)→0
x2+y2		x2+y2		x2+y2

granica funkcji jest rowna 0 (na mocy tw. o trzech funkcjach) dobrze?

mto: 1) nie istnieje bo równa się na końcu sin*cos, wystarczy dobrać współrzędne tak aby x=y i i zbadać funkcję w f(0,y) , lub f(x,0) i widać że granice są różne

zadanie: ale bez tego tez jest dobrze?

mto: w 2 można jeszcze z tw analogicznego do tw o 3 ciągach widzisz to ?

mto: a co byś powiedział o takim zadaniu : [ apropos 1) ]

	x3
limx−>0,y−>0
	x2+y2

mto: aha i 3,dlaczego szacujesz sinusa przez x i y w 4 potędze a nie prze 1 ?

zadanie: 23:49 sprobowalbym zastosowac wspolrzedne biegunowe 23:51 korzystam z nierownosci |sint|≤|t|

zadanie: a jakby to 2 wygladalo z tego twierdzenia?

mto: no właśnie jak dla tw o 3 funkcjach tylko sinus przez jedynkę, ale pomocniejsze będzie zastosować podstawienie pod x i y osobno wartosci i sprawdzenie że pędzi do różnych granic

mto: a skąd masz to ograniczenie |sint|≤|t| sorki nie pamiętam tego

zadanie: z ksiazki

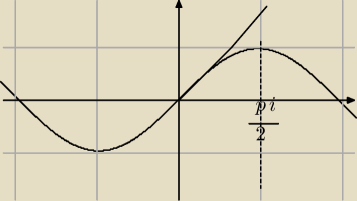
mto: no to spoko fajnie jak byś tytuł podał, pamiętam że przy pochodnych było takie dowodzenia ale dla dużych wartości |sin(x)|≤|x|