Dane są punkty A(-1, 1) i B(5, -1). Na symetralnej odcinka AB znajdź taki punkt Col.: Dane są punkty A(−1, 1) i B(5, −1). Na symetralnej odcinka AB znajdź taki punkt C, dla którego pole trójkąta ABC jest równe 30. Następnie oblicz obwód trójkąta ABC. Proszę o pomoc i w miarę możliwości, szczegółowe wytłumaczenie. Z góry dziękuję

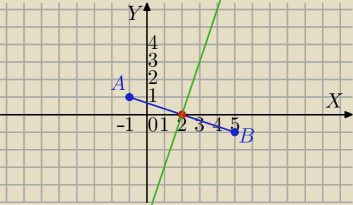
Mila: |AB|=√2²+6²=√40=2√10

	1
PΔ=		|AB|*h⇔
	2

1
	*2√10*h=30⇔
2

	30		30*√10
h=		=		=3√10
	√10		10

h=3√10 =======

	−1+5		1+(−1)
S=(		,		)=(2,0) środek odcinka AB
	2		2

Symetralna dzieli AB na połowy i jest prostopadła do AB. Symetralna odcinka jest zbiorem wszystkich punktów jednakowo odległych od końców odcinka. Skorzystamy z drugiej własności:⇔ P(x,y) dowolny punkt symetralnej. √(x+1)²+(y−1)²=√(x−5)²+(y+1)² /² po przekształceniach (wykonaj sam) s: y=3x−6 C=(x_c,y_c) wsp. szukanego punktu, C∊s C=(x_c,3x_c−6) |SC|=√(x_c−2)²+(3x_c−6−0)²=h ⇔ √(x_c−2)²+(3x_c−6−0)²=3√10 /² (x_c−2)²+(3x_c−6−0)²=9*10 dokończysz ?, otrzymasz 2 rozwiązania

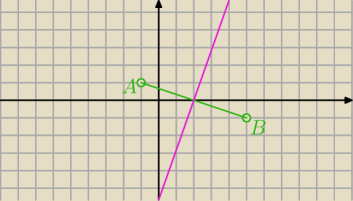
===: |AB|=√4+36=2√10 30=0,5h*2√10 ⇒ h=.... h jest jednocześnie odległością punktu C od prostej przechodzącej przez A i B

Col.: Dzięki za odpowiedź. Ale mam jeszcze pytanie: skąd dokładnie wzięło się y=3x−6? 3 to współczynnik kierunkowy, wnioskując po odpowiedziach z innych stron dotyczących zadania, ale skąd się tam wziął i czym dokładnie jest −6? Są to niestety jedyne elementy, których nie rozumiem w tym zadaniu.

Mila: Masz tam napisane : "po przekształceniach... Podnieś obie strony do kwadratu, wykonaj potęgowanie (Wzory skróconego mnożenia), y=3x−6 to równanie symetralnej odcinka − to prosta

Mila: