jaki jJaki jest kąt między przekątnymi w trapezie równoramiennym? zaza: bok kwadratu ABCD ma dłógość 16cm. Punkty EiF są środkami boków AB i BC. Oblicz pole trójkąta DEF. Jaką cześcią pola kwadratu ABCD jest tego trójkątaprosze o pomoc

Godzio: Pole kwadratu P_k=16²

	8*16
2P1=2*
	2

	8*8
P2=
	2

P_k−2P₁−P₂= P_Δ oblicz

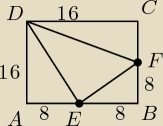
Matematyk: Nie jest to zbyt skomplikowane. Rysujesz kwadrat i zaznaczasz punkty E i F. Skoro są środkami boków, to odcinki EB i BF są równe i mają po 8 cm. Twierdzenie Pitagorasa: 8²+8²=c² (c to bok EF) 128=c² √128=c 8*√2=c Teraz mamy podstawę trójkąta, potrzebna jest wysokość. Trójkąty DCF i AED są takie same, czyli DEF jest trójkątem równoramiennym. Wysokość z punktu D podzieli EF na połowy i zarazem stworzy trójkąt prostokątny− mamy jego jeden bok, potrzebny jest jeszcze DE lub DF(to nie ma znaczenia, przecież to trójkąt równoramienny). Dokończ sama, jak będą problemy to pisz, ale teraz to już zostało mało do zrobienia. Możesz jeszcze napisać, dlaczego DE i DF mają równe długości(raczej jest to wymagane, zostawię to Tobie−musisz coś z tego wynieść).

Matematyk: Chyba zostałem uprzedzony, bardzo przepraszam.

Godzio: nie ma za co

zaza: wielkie dzieki

zaza: prosze jeszcze pisac odpowiedzi

Godzio: 256−128−32=96 = P_Δ

96		3
	=
256		8

zaza: fęks

zaza: podaj wzur

Godzio: jaki ?

Godzio: wzór

zaza: przepraszaM JAK OBICZYŁEŚ 256

Rajc z Nakło nad Notecia POZDR: Siemka fajne zadanie nie wiem czy dobrze rozwiązane ale dzięki może się przyda...Δ

Rajc z Nakło nad Notecia POZDR: NO racja... w mojej książce też tak piszę... z tyłu w odp...

RajcXdd: ∑≥≤→→∑∫≥→≠←≥⇔