proszę Radzio: Bardzo Proszę o pomoc. Na przeciwprostokątnej AB trójkąta prostokątnego ABC obrano punkty D i E takie, że |AD=|AC| oraz |BE| = |BC|. Wykaż, że | kąt DCE| = 45 stopni

Basia: Pomagam

wmboczek: α,β−kąty przy A,B α+β=90 odłożono przyprostokątne na przeciwprostokątnej − 2 trójkąty równoramienne (180−α)/2 i (180−β)/2 z 90 przy C zostało 90−(180−α)/2 z jednej i 90−(180−β)/2 z drugiej strony czyli α/2+β/2=45

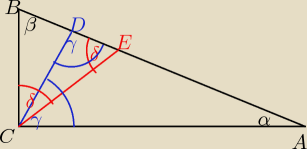
Basia: α+β=90

	180−α		α
AC=AD ⇒ 2y = 180−α ⇒ γ=		= 90 −
	2		2

	180−β		β
BC=BE ⇒ 2δ= 180−β ⇒ δ=		= 90 −
	2		2

	α		β		α+β		90
∡DCE = 180 − γ − δ = 180 − 90 +		− 90 +		=		=		=45
	2		2		2		2