funkcje i parametr Miśka: narysuj wykres funkcji f(x) = x²−|4x−4|=m posługując się wykresem funkcji f(x) odczytaj liczbe rozwiązań równania w zależności od parametru m

ZKS: Rozbij wartość bezwzględną.

bezendu: m∊(−∞,−8) brak rozwiązań m{−8} jedno rozwiązanie m∊(−8,0)∪(1,∞) dwa rozwiązania m∊{0,1} trzy rozwiązania m∊(0,1) cztery rozwiązania

Miśka: a mogę prosić o mały komentarz

Godzio : m − to proste y = m, jeden punkt przecięcia się takiej prostej z wykresem to jedno rozwiązanie Wykres rysujesz dzieląc na przypadki: 4x − 4 ≥ 0 i < 0

Miśka: a na jakiej podstawie zrobić te przedziały?

52: Odczytujesz z osi OY

Miśka: ale jeszcze pytanie jak zacząć? f(x) = x2−|4x−4|=m y(x)=x²−4x−4=m i tu jakoś z delty? prosze rozpisz mi to ...

52: hmmm No to musisz wiedzieć jak narysować wykres Zapisz f(x) w dwóch przedziałach 1. x∊(−∞,1) 2.x∊<1,+∞) f(x)=x²−(−4x+4) f(x)=x²−(4x−4) f(x)=x²+4x−4 f(x)=x²−4x+4 I powinnaś uzyskać taki sam wykres jak narysował bezendu I teraz patrzysz na to co ci napisał Godzio

Miśka: i z tych funkcji obliczyć msca zerowe?

52: Nie, w tych przedziałach rysujesz funkcje takie jakie wyszły I przyłóż linijkę równolegle do osi OX i tak nią ruszaj i patrz ile razy w danym punkcie (0,y) przecina ci wykres... Nie wiem jak to ładnie napisać abyś zrozumiała....

Miśka: a możesz mi jeszcze obliczyć x2−|4x−4|−4>=0

Miśka: okej ale skąd wiesz gdzie będzie przecięcie OX?

Godzio : Zaraz Ci napiszę co i jak.

Miśka: <3 dzięki

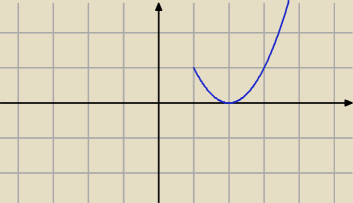
Godzio : narysuj wykres funkcji f(x) = x2−|4x−4|=m posługując się wykresem funkcji f(x) odczytaj liczbe rozwiązań równania w zależności od parametru m f(x) = x² − |4x − 4| Przypadek pierwszy: 4x − 4 ≥ 0 ⇔ 4x ≥ 4 ⇔ x ≥ 1. Wówczas f(x) = x² − 4x + 4 = (x − 2)² −− parabola o wierzchołku (2,0)

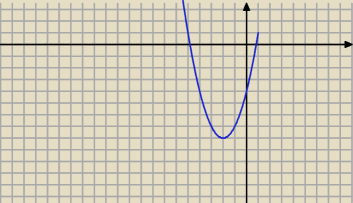
Godzio : Przypadek drugi: 4x − 4 < 0 ⇔ 4x < 4 ⇔ x < 1. Wówczas f(x) = x² + 4x − 4 = x² + 4x + 4 − 8 = (x + 2)² − 8 −− parabola o wierzchołku (−2,−8) i miejscach zerowych x₁ = − 2 − 2√2 i x₂ = −2 + 2√2

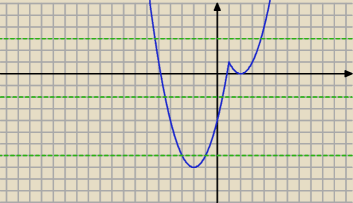
Godzio : Ostatecznie:

	⎧	x2 − 4x + 4 gdy x ≥ 1
f(x) =	⎩	x2 + 4x − 4 gdy x < 1

Teraz prowadzimy sobie proste y = m i odczytujemy ilość punktów przecięcia w zależności od m. No i np. Dla m = −8 (najniższy wierzchołek) mamy jeden punkt przecięcia = jedno rozwiązanie Jasne?

Miśka: jasne