funkcje arem: 1) Suma kwadratów wielomianu w(x) = ax³ − 6ax² + (5a + 6)x − 6 jest równa 14. Wyznacz parametr a oraz pierwiastki tego wielomianu, jeżeli jego współczynni są liczbami całkowitymi. 2) Punkty A i B są punktami przecięcia okręgu (x − 2)² + (y + 1)² = 25 z prostą y = −2x+8, a odcinek AC jest średnicą tego okręgu. Oblicz pole trójkąta ABC, jeśli punkt A ma obie współrzędne dodatnie. 3) Na rysunku obok przedstawiono wykres funkcji f(x) = log_ax Oblicz a Naszkicuj wykres funkcji g(x) = |f(x+1)−2| i wyznacz dodatnią liczbę x, dla której spełniona jset równość g(0)=g(x) za moment dodam wykres. Proszę o rozwiązanie tych zadań.

arem: Wykres funkcji: http://bankfotek.pl/image/1805414.jpeg

Janek191: Popraw treść z. 1

arem: 1) Suma kwadratów pierwiastków wielomianu w(x) = ax³ − 6ax² + (5a + 6)x − 6 jest równa 14. Wyznacz parametr a oraz pierwiastki tego wielomianu, jeżeli jego współczynniki są liczbami całkowitymi.

Hurwitz: Ad. 1. zastosuj wzory Viete'a.

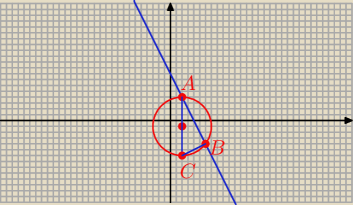
Janek191: z.2 ( x − 2)² + ( y + 1)² = 25 ⇒ S = ( 2 ; − 1) r = 5 y = − 2 x + 8 Trzeba rozwiązać ten układ: x² − 4 x + 4 + ( − 2 x + 8 + 1)² = 25 x² − 4 x + 4 + 4 x² − 36 x + 81 = 25 5 x² − 40 x + 60 = 0 / : 5 x² − 8 x + 12 = 0 ( x − 2)*( x − 6) = 0 x = 2 lub x = 6 więc y = −2*2 + 8 = 4 lub y = −2*6 + 8 = − 4 czyli A = ( 2; 4) B = ( 6 ; − 4) ======================= oraz C = ( 2; − 1 − 5) = ( 2 ; − 6) Pole Δ_ABC P = 0,5*I ABI*I BCI, bo ten trójkąt jest prostokątny. Dokończ:

J : 3) Wykres sugeruje,ze f(x) = log₂x ( chociaż nie jest zbyt dokładny).. w takim razie : f(x+1) = log₂(x+1) g(x) = Ilog₂(x+1) −2I rysyjesz wykres funkcji: log−_x i przesuwasz o wektor v = [−1,−2] , nastepnie to co pod osią OX odbijasz wzgledem tej osi .... g(0) = Ilog₂(0 +1) − 2I = I log₂1 − 2I = I 0 −2 I = I−2I = 2 g(x) = 2 ⇔ Ilog₂(x+1) −2I = 2 ⇔ log₂(x+1) −2 = 2 lub log₂(x+1) −2 = − 2 ⇔ ⇔ log₂(x+1) = 4 lub log₂(x+1) = 0 ⇔ x+1 = 16 lub x +1 = 1 ⇔ x = 15 lub x = 0 (odpada)

J : ...rysujesz wykres funkcji: log₂x i przesuwasz....