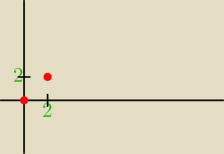
surjekcja komik: czy narysowana funkcja jest surjekcją ? nie moge zrozumieć pojęcia surjekcji, proszę o wyjaśnienie.

J : ... to zależy, jak jest określona dziedzina i przeciwdziedzina tej funkcji...

Hurwitz: Dziedzina jest podana: {0,2}. Odpowiedź zależy od zbioru wartości.

Janek191: na Suriekcja f: X → Y Musi zachodzić: Y = f( X ) Def. Funkcję f: X → Y nazywamy suriekcją ,jeżeli przeciwobraz każdego y ∊ Y składa się co najmniej z jednego punktu.

Janek191: Pytanie − czy f = { ( 0;0) , (2 ; 2) } ?

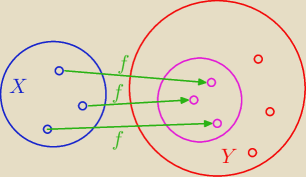
Janek191: w Iniekcja f : X → Y f(X) ⊂ Y

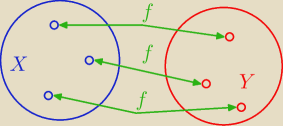
Janek191: Bijekcja f: X → Y ≈ Y = f( X) Def. Funkcję f : X → Y nazywamy bijekcją , jeżeli przeciwobraz każdego y ∊ Y sklada się dokładnie z jednego punktu. −−−−−−− Bijekcja to przekształcenie wzajemnie jednoznaczne : 1 do 1

Hurwitz: Jeżeli Twoja funkcja to f:{0,2}→{0,2} to jest to surjekcja. Jeżeli Twoja funkcja to f:{0,2}→N (N− liczby naturalne) to nie jest surjekcją. Surjekcja to funkcja, która wypełnia zbiór wartości: nie istnieje y, który nie jest uzyskane za pomocą funkcji f z pewnego x.

Janek191: Używa się zapisu " suriekcja " lub " surjekcja ". Prof. dr Tadeusz Trajdos pisze : suriekcja

Hurwitz: Nie spotkałem się z "suriekcją". Podobnie jak z "iniekcją" (w matematyce; nie mam na myśli zastrzyków). Ale kto wie... Jest bałagan; nawet w słowniku języka polskiego PWN nie mogą się zdecydować co i jak.

J : .... suriekcja jest też poprawną formą ....

b.: > nie moge zrozumieć pojęcia surjekcji Żeby je zrozumieć, trzeba rozumieć pojęcie funkcji W szczególności, że funkcja zawsze ma jakąś daną dziedzinę i przeciwdziedzinę. Na przykład, zapisy typu: (1) niech funkcja f będzie zadana wzorem f(x)=x², albo (2) niech funkcja f będzie zadana wzorem f(x)=x² dla x∊R są formalnie biorąc nieprecyzyjne. Powinno być np. (3) niech f:R−>R będzie zadana wzorem f(x)=x² dla x∊R. I wtedy jest jasne, czy to surjekcja czy nie. A jak funkcja jest zadana przez jakiś wykres na obrazku, to odpowiada to zapisowi (1) lub (2), więc nie jest wystarczająco precyzyjne do udzielenia odpowiedzi na pytanie, czy funkcja ta jest surjekcją.

J : ...post: 8:20 ...