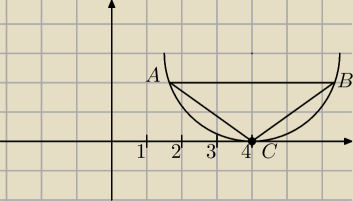
Równanie kierunkowe prostej olkaq: Hej. Pomoże mi ktoś z takim zadanie? Dwa wierzchołki trójkąta równoramiennego ABC znajdują się

	1
na paraboli o równanie y =		(x − 4)2, zaś trzecim wierzchołkiem trójkąta jest
	4

wierzchołek paraboli. Wyznacz współrzędne wierzchołków tego trójkąta, jeśli wiadomo że kąt rozwarty tego trójkąta ma miarę 120^o Z wiadomości zadania wywnioskowałam że współrzędne punktu C = (4,0) A współrzędne punktów A i B można zapisać jako: A = (x_A − 4, y_A) B = (x_B − 4, y_A) Niestety nie wiem jak dalej można by to pociągnąć

olkaq:

olkaq:

ICSP: skoro ∡ACB = 120^o to ∡CAB = 30^o. Dodatkowo punkt A należy do paraboli, więc ma współrzędne:

	1
A(xa ,		(xa − 4)2)
	4

	|CD|
niech D będzie środkiem odcinka AB. wtedy		= tg30o
	|AD|

	1
Zauważ, że |AD| = |4 − xa| oraz |CD| =		(xa − 4)2
	4

stąd :

(xa − 4)2		√3
	=
4|4 − xa|		3

	4
skąd xa = 4 ±
	√3

	4
Ustalmy,że punkt A ma odciętą mniejszą od odciętej wierzchołka. Wtedy xa = 4 −
	√3

	4
oraz xb = 4 +
	√3

Ostatecznie :

	4		4
A( 4 −		,		)
	√3		3

	4		4
B( 4 +		,		)
	√3		3

ICSP: Oczywiście x_a ≠ 4, nie chcemy Aby punkt A był punktem C.