 x>0
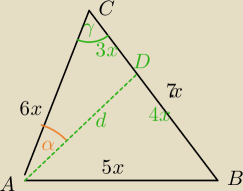
Z tw. cosinusów w ΔABC:
(5x)2=(6x)2+(7x)2−2*6*7x2*cosγ
25x2=36x2+49x2−84x2cosγ /:x2
60=84 *cosγ
x>0
Z tw. cosinusów w ΔABC:
(5x)2=(6x)2+(7x)2−2*6*7x2*cosγ
25x2=36x2+49x2−84x2cosγ /:x2
60=84 *cosγ
| 60 | ||
cosγ= | ||
| 84 |
| 15 | 5 | |||
cosγ= | = | |||
| 21 | 7 |
| 2√6 | ||
z jedynki tryg. sinγ= | ||
| 7 |
| 5 | ||
d2=(6x)2+(3x)2−2*6x*3x* | ||
| 7 |
| 180 | ||
d2=36x2+9x2− | x2 | |
| 7 |
| 5 | ||
d2=45x2−25 | x2 | |
| 7 |
| 2 | 135 | |||
d2=19 | x2= | x2 | ||
| 7 | 7 |
| 3√15 | ||
d= | ||
| √7 |
| 3x | d | ||
= | |||
| sinα | sinγ |