Ratunku !! Kasiekk: Znajdź wzór funkcji, której wykresem jest hiperbola o asymptocie poziomej y=4 przecinająca os OY w punkcie (0,6) i przechodząca przez punkt (4,1) Proszę o rozwiązanie tego z układu równań i podanie szczegółowego rozwiązania

Kasiekk: Haloo?

Kasiekk: Noo Bogdan? albo ktos inny?

': nie wiem jak asymptota pozioma y=4 może przecinać OY w punkcie (0,6) ?

Nikka: nie asymptota, tylko hiperbola przecina oś OY w punkcie (0,6)...

Kasiekk: os OX przepraszam

Kasiekk: ale polecenie mam z osia OY

Kasiekk: Znajdź wzór funkcji, której wykresem jest hiperbola o asymptocie poziomej y=4 przecinająca os OY w punkcie (0,6) i przechodząca przez punkt (4,1) na 100% takie

Nikka: treść zadania jest raczej ok

Kasiekk: ja to robiłam tak, ale nie wiem czy dobrze:

	a
y=		+q
	x−p

asymptota pozioma y=4 oś OY: (0,6) pkt: (4,1)

	a
6=		+4 / (−p)
	−p

	a
1=		+4 / (4−p)
	4−p

−6p=a−4p 4−p=a+16−4p −2p=a / (−1) 3p=a+12 2p=−a 3p=a+12 + −−−−−−−−−−−−−−−− 3p+2p=a+12−a

	2
p=2
	5

	4
a=−4
	5

ale nie wiem czy dobrze myśle

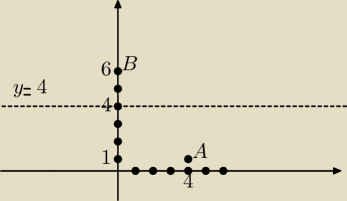
': Jeżeli hiperbola przechodzi przez A i B to y=4 nie będzie jej asymptotą

Kasiekk: no to ja już nie wiem. Treść zadania jest na pewno dobra

Nikka:

	a
Postać kanoniczna funkcji homograficznej to f(x) =		+ q
	x−p

D_f = R\{p} x=p − równanie asymptoty pionowej ZW_f = R\{q} y=q − równanie asymptoty poziomej y=4 − asymptota pozioma czyli

	a
f(x) =		+ 4
	x−p

Hiperbola przechodzi przez dwa punkty: (0,6) i (4,1). Stąd

	a
6 =		+ 4
	0−p

	a
1 =		+ 4
	4−p

Rozwiązując układ równań obliczamy a i p:

	12
p =
	5

	24
a = −
	5

Wracamy do wzoru funkcji:

	24   −   5
f(x) =		+ 4
	12   x−   5

	−24
f(x) =		+ 4
	5x−12

Kasiekk: czyli to co mi wyszlo z układu równań podstawiam pod wzór funkcji? wszystko tzn x y p q ?

Nikka: skoro mamy te same wyniki to jest ok

Nikka: podstawiasz tylko a, p, q

Kasiekk: no to super ; dziekuje za pomoc

Nikka: proszę

AROB:

	a
Wszystko się zgadza. Czyli : y =		+ q
	x−p

	24   −   5
y =		+ 4
	12   x −   5