PROSZE O POMOC magdziaf: 1. Dana jest prosta k: y = –x + 6, która przecina oś OY w punkcie A. Przez punkt P(4, 2) poprowadzono prostą l, która przecięła oś OY powyżej punktu (0, 2) i poniżej punktu A. Suma pól dwóch trójkątów powstałych między prostymi k, l oraz osiami układu współrzędnych jest równa 6. Napisz równanie prostej l. 2. Dana jest prosta k: y = –x + 6, która przecina oś OY w punkcie A. Przez punkt P(2, 4) poprowadzono prostą l, która przecięła oś OY powyżej punktu A. Suma pól dwóch trójkątów powstałych między prostymi k, l oraz osiami układu współrzędnych jest równa 6. Napisz równanie prostej l. 3. Punkty A(–2, –3), B(0, –5) są kolejnymi wierzchołkami kwadratu ABCD, a punkt S(0, –3) jest środkiem symetrii tego kwadratu. a) Oblicz współrzędne pozostałych wierzchołków kwadratu. b) Oblicz pole kwadratu. c) Jakim procentem pola kwadratu jest pole koła opisanego na tym kwadracie? Zaokrąglij liczbę π ≈ 3,1415… do drugiego miejsca po przecinku. a) D(0,−1) , C(2,−3) b)P=8

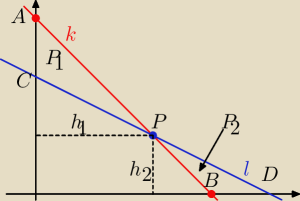
Janek191: k : y = − x + 6 więc A = ( 0; 6) B = ( 6 ; 0) P = ( 4 ; 2) oraz C = ( 0; b₁) D = ( a₁ ; 0) więc P₁ = 0,5*I AC I*h₁ = 0,5*( 6 − b₁)*4 = 2*( 6 − b₁) P₂ = 0,5*I BD I*h₂ = 0,5*a₁ − 6)*2 = a₁ − 6 zatem 2*( 6 − b₁) + (a₁ − 6) = 6 12 − 2 b₁ + a₁ = 12 a₁ − 2 b₁ = 0 a₁ = 2 b₁ dlatego C = ( 0; b₁) D = ( 2 b₁; 0) Współczynnik kierunkowy prostej l :

	0 − b1
a =		= − 0,5
	2 b1 − 0

l : y = − 0,5 x + m Prosta l przechodzi przez punkt P= ( 4; 2), więc 2 = − 0,5*4 + m m = 4 Odp. l : y = − 0,5 x + 4 =====================

Janek191: A = ( − 2; − 3) B = ( 0 ; − 5) S = ( 0 ; − 3) S jest środkiem odcinka AC i środkiem odcinka BD. Niech C = ( a ; b) więc

− 2 + a		− 3 + b
	= 0 i		= − 3
2		2

a = 2 − 3 + b = − 6 ⇒ b = − 3 czyli C = ( 2 ; − 3) ========== D = ( c ; d) więc

0 + c		− 5 + d
	= 0 i		= − 3
2		2

c = 0 − 5 + d = − 6 ⇒ d = − 1 czyli D = ( 0 ; − 1) ==========

Janek191: b) Pole kwadratu : P = 0,5* I AC I* I BD I = 0,5*(2 − (−2))*( − 1 − (− 5)) = 0,5*4*4 = 8