funkcja kwadratowa inqqq : Funkcja kwadratowa f opisana wzorem f(x)=−0,5x² +x+a²−4 , gdzie a jest parametrem (a∊R) a) wykaż na podstawie definicji, że funkcja jest malejąca w przedziale (1+∞) dla dowolnego a ∊R b) wyznacz wartość parametru a, wiedząc, że różnica miejsc zerowych funkcji f wynosi 10

Janek191: a) f(x) = − 0,5 x² + x + a² − 4; a ∊ℛ −0,5 < 0 więc ramiona paraboli są skierowane ku dołowi

	b		− 1
p = −		=		= 1
	2a		2* 9−0,5)

zatem f maleje w przedziale ( 1 ; + ∞ ) b) x₁ − x₂ = 10 więc

− b − √Δ		− b + √Δ
	−		= 2√Δ = 10 ⇒ √Δ = 5 ⇒ Δ = 25
− 1		− 1

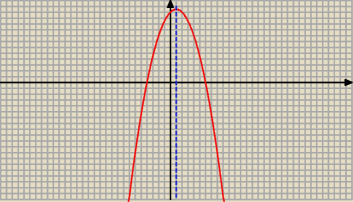
1 − 4*(−0,5)*( a² − 4) = 25 1 + 2*(a² − 4) = 25 2a² − 8 = 24 a² − 4 = 12 a² = 16 a = − 4 lub a = 4 =============== Dodatkowo − wykres funkcji dla a² = 16

J: ad a) ... to nie jest wykazanie monotoniczności na podstawie definicji...