Funkcja wymierna z wartością bezwzględną
Szczepan: Witajcie, mam problemy z funkcjami, w których jest wartość bezwzględna... Mianowicie chodzi o
naszkicowanie wykresu funkcji
a następnie naszkicowaniu wykresu funkcji g, która każdej wartości parametru m przyporządkowuje
liczbę rozwiązań f(x)=m.
A więc ja do tego zabrałem się tak:
1.
D=R\{−1}
| | x−3 | |
f(x)= |
| , dla x−3≥0, czyli x≥3 |
| | x+1 | |
| | x−3 | | x+1−4 | | −4 | |
f(x)= |
| = |
| = |
| +1 |
| | x+1 | | x+1 | | x+1 | |
2.
| | −x+3 | |
f(x)= |
| , dla x−3<0, czyli x<3 |
| | x+1 | |
| | −x+3 | | −x−1+4 | | −1(x+1 | | 4 | | 4 | |
f(x)= |
| = |
| = |
| + |
| = |
| −1 |
| | x+1 | | x+1 | | x+1 | | x+1 | | x+1 | |
i jak po tym zabrać się do rysowania? Ja zrobiłem to tak:
| −4 | | −4 | |
| →w=[−1,1]→ |
| +1 ,dla x≥3 |
| x | | x+1 | |
oraz
| 4 | | 4 | |
| →w=[−1,−1]→ |
| −1 ,dla x<3 |
| x | | x+1 | |
Później zrobiłem dwie tabelki, jedna dla x równego 3,4,6,8,12, drugą dla −4,−2,−1,0,1,2,
później przesunąłem odpowiednio oraz wykluczyłem punkt, który nie spełnia warunków dziedziny,
no i niestety wykres nie wygląda tak jak powinien (sprawdziłem w generatorze online).
Co robię źle oraz jak zabrać się do drugiej części zadania?
22 paź 23:09
Tadeusz:
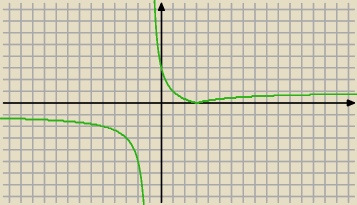
22 paź 23:15
Szczepan: Wiem, że to ma tak wyglądać (pisałem, że sprawdziłem w generatorze

), ale nie wiem sam, jak
to narysować. Wszystkie kroki do momentu rysowania są dobrze?
22 paź 23:16
Tadeusz: tak
22 paź 23:17
Szczepan: To jak najlepiej rysować tego typu wykresy?
22 paź 23:18
Tadeusz:
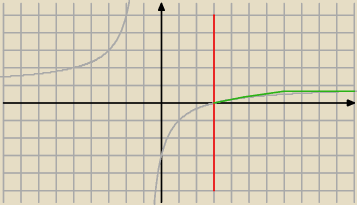
dla x≥3
22 paź 23:23
Szczepan: Okej, rozumiem.Tak jakby "odciąłem" tę część z lewej przed przesunięciem, a nie po przesunięciu
i funkcja dla x≥3 zaczynała się tak na prawdę od x=2... Dlatego nachodziły mi się na siebie
częściowo funkcje.
Trochę głupi błąd, ale teraz na pewno zapamiętam

Dzięki wielkie i dobrej nocy życzę

22 paź 23:27
Szczepan: Tzn wróć... Nie dobrej, nie dobrej

Jeszcze dalsza część polecenia. Jak to ma wyglądać?
22 paź 23:28
Tadeusz:
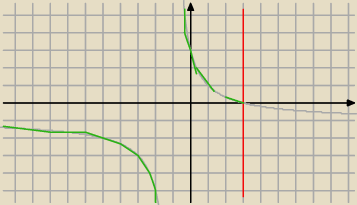
dla x<3
i składasz
22 paź 23:28
Tadeusz:
... a teraz "tnij" wykres poziomą−

22 paź 23:29
Tadeusz:
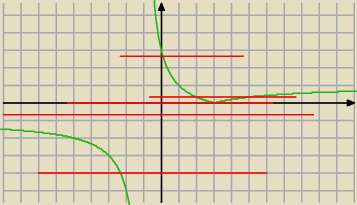
22 paź 23:32
Szczepan: Czyli rysuję po prostu prostą, gdzie w przedziale:
(−∞,−1) jest to y=1,
dla x=−1 brak,
(−1,1) y=1
i dla (−2,∞) y=2?
22 paź 23:33
Szczepan: A nie, między y=−1, a 0 nie ma rozwiązań

To jak to zapisać?
22 paź 23:34
Tadeusz:
(−∞, −1)......1
<−1, 0) ......0
0 1
(0, 1) 2
<1, ∞) 1
22 paź 23:38
Szczepan: Tak teraz sobie w zeszycie właśnie napisałem.

Także...
Panie Tadeuszu, jest Pan wielkie!

Dziękuję i życzę dobrej nocy

22 paź 23:40
Tadeusz:
−

wzajemnie
22 paź 23:42

 ), ale nie wiem sam, jak
to narysować. Wszystkie kroki do momentu rysowania są dobrze?
), ale nie wiem sam, jak
to narysować. Wszystkie kroki do momentu rysowania są dobrze?
 dla x≥3
dla x≥3
 Dzięki wielkie i dobrej nocy życzę
Dzięki wielkie i dobrej nocy życzę 
 Jeszcze dalsza część polecenia. Jak to ma wyglądać?
Jeszcze dalsza część polecenia. Jak to ma wyglądać?
 dla x<3
i składasz
dla x<3
i składasz


 To jak to zapisać?
To jak to zapisać?
 Także...
Panie Tadeuszu, jest Pan wielkie!
Także...
Panie Tadeuszu, jest Pan wielkie!  Dziękuję i życzę dobrej nocy
Dziękuję i życzę dobrej nocy 
 wzajemnie
wzajemnie