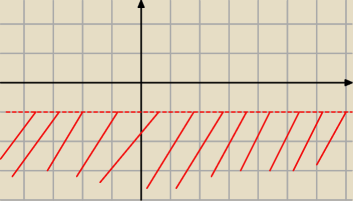
zespolone 3 Lukas: Znajdź wszystkie liczby zespolone spełniające podane warunki Re(iz)≥1 Re(xi−y)≥1 y≤−1

52: Re(iz)≥1 z=x+yi iz=ix+yi²=ix−y Re(iz)=−y −y≥1 y≤−1 ... Czyli dobrze...

52: Tylko że linia ciągła na rysunku, a nie przerywana...

Lukas: To jest drobny szczegół, punkty leżące na prostej należą do rozwiązania. to samo polecenie

	z+2		3z+i
b)		=
	i−1		2+1

	19		25i
wyszło mi z=−		−		?
	29		29

52: Prawy mianownik to 2+1 ?

Lukas: 2+i

bezendu: Dobrze masz.

Lukas: c) Im(z²)=(2−i)z Im(x²+2xyi−y²)=2z−zi Im[(x²−y²)+2xyi]=2x+2yi−xi−y 2xy=(2x−y)+(2y−x)i 2xy=2x−y 2y−x=0 ⇒x=2y 2(2y)y=2(2y)−y 4y²−3y=0 y(4y−3)=0

	3
y=0 lub y=
	4

z=0 lub z₁=1,5+0,75i ?

Lukas: ?

Lukas: ?

MQ: −zi=−(x+iy)i=−xi+y popraw w 3 linijce

Lukas: Im[(x²+2xyi−y²]=2x+2yi−xi+y 2xy=(2x+y)+(2y−x)i 2xy=2x+y 2y−x=0⇒x=2y 4y²−5y=0 y(4y−5)=0

	5
y=0 lub y=
	4

z₁=0

	5i
z2=2,5+
	4

Lukas: ?

Lukas: ?

Mila: W porządku, dobrze.

Lukas: ale tego za chiny nie wiem jak zrobić z+1=x+1−yi x+yi+1=x+1−yi (x+1)+yi=(x+1)−yi x+1=x+1 tożsamość y=−y ? ostatecznie ?

Kacper: z+1=x+1−yi ? ile tych niewiadomych masz?

Lukas: Po prawej stronie jest ale od razu to rozpisałem

Mila: x+iy+1=(x+iy+1)⁻⇔ (x+1)+iy=(x+1)−iy x+1=x+1 dla każdego x∊R i 2y=0⇔y=0 Oś OX

Lukas: czyli z=x ? x∊R ?

Mila:

Lukas: Dziękuję, jeszcze dużo zadań przede mną

Lukas: ż=sprzężenie d) z+ż+(z−ż)i=5+3i x+yi+x−yi−2y=5+3i 2x−2y=5 ?

Lukas: ?

Mila: Tak

Lukas: To nie ma rozwiązania x,y ∊∅

Lukas: Oblicz moduł

(3−√3i)2
(√2+2i)3

|z|=U{√609{29}

	√6
w odpowiedzi
	3

Mila: Do przykladu (d) jaką masz odpowiedź w książe? Ostatni liczę.

Mila: 21:54 wychodzi ładnie tak jak w odpowiedzi.

Lukas: Nie mam odpowiedzi do d) Jak rozpisuję zadanie 21:51

	10√3−6
U{−15−4√3{29}+		i
	29

i moduł nie wychodzi tak jak w książce

Mila:

(3−√3i)2
	= taka liczba? W mianowniku: (√2+2i)3
(√2+2i)3

Lukas: Tak, taka liczba.

Mila: d) dokończenie: x+yi+x−yi−2y=5+3i (2x−2y )+0*i=5+3i 2x−2y=5 0=3 sprzeczność − brak rozwiązań

Mila:

(9−6√3i−3
	=
2√2+3*2*2i+3*√2*(2i)2+(2i)3

	6−6√3i		6−6√3i		3−3√3i
=		=		=
	2√2+12i−12√2−8i		−10√2+4i		−5√2+2i

	3−3√3i		√32+(3√3)2		√36
|		|=		=		=
	−5√2+2i		√(5√2)2+22		√54

	6		6√6		√6
=		=		=
	3√6		3*6		3

Lukas: hmm ja zrobiłem tak :

6−6√3i		3−3√2i
	=
−10+4i		−5−2i

i potem pomnożyłem przez sprzężenie −5+2i i nie wyszło poprawnie, nie wiedziałem, że można osobno liczyć dla liczniki i osobno dla mianownika.

Mila: Też powinno Ci wyjśc: opuściłeś √2 przy 10.

Lukas:

	3−3√2i
Tak wiem, że powinno być		ale mnożąc przez sprzężenie −5√2+2i i tak nie
	−5√2−2i

wychodzi odpowiedni moduł.

J : ...popraw licznik ... 3 − 3√3i

Lukas: Ok, teraz wyszło.