prosze pomóżcie. Agnieszka: Na trójkącie ABC opisano okrąg o środku w punkcie O. a.) Oblicz miary kątów trójkąta ABC wiedząc, że |∡AOB|=100 stopni oraz 3*|∡BOC|=10*|∡AOC| b.) przyjmując, że promień okręgu ma 10 cm długości oblicz |AC| i odległość punktu O od boku AC

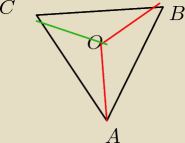
[N[Mariusz]]: ABBCO a) AOB=100 3*BOC=10*AOC

	10
BOC=		AOC
	3

AOC+BOC=260 bo 360−100 13/3 AOC=260 AOC=60 BOC=200

Agnieszka: dlaczego 13/3? i jak zrobić b.)?

Godzio:

	10		3		10		13
chodzi o to ze kąt AOC +		AOC =		AOC +		AOC =		AOC
	3		3		3		3

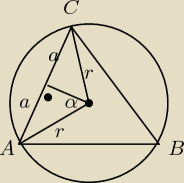
Godzio: r=10 wiemy że AOC = 60^o czyli α=30^o

	a
sinα=
	r

	1
a=		*10
	2

a=5 AC=2a=10 cm

	a
tgα=
	h

	5		15√3
h=		=		=5√3
	√3   3		3

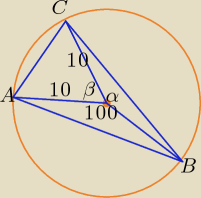
Bogdan: Można uprościć rozwiązanie tego zadania np. tak:

	3
3α = 10β ⇒ β =		α
	10

	3		13		10
100o + α +		α = 360o ⇒		α = 260o / *		⇒ α = 200o
	10		10		13

	3
β =		* 200 = 60o.
	10

Skoro β = 60^o, to trójkąt AOC jest równoboczny, stąd każdy bok tego trójkąta ma długość 10, w tym |AC| = 10. Odległość od środka okręgu O od boku AC jest wysokością w tym trójkącie równobocznym

	1
i jest równa		*10√3 = 5√3
	2

Agnieszka: dziękuję

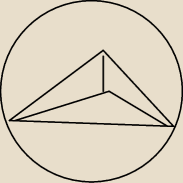
trara: na trójkącie ABC opisany jest okrąg o środku w punkcie O.Oblicz miary kątów tego trójkąta

trara: miary katow to 50 i 150