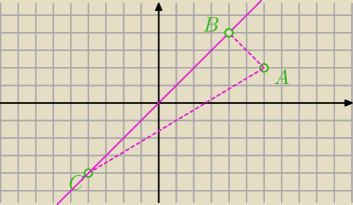
hej :D halohalo: punkty A(6,2) i C(−4,−4) sa wierzchołkami trójkata równoramiennego ABC, w którym |AC|=|BC|. wysokosc poprowadzona z wierzchołka C zawiera się w prostej k: x−y=0. Oblicz: a) współrzedne wierzchołka B b) pole trójkata ABC prosze o pomoc

===: B(x_B, y_B) Jedno równanie na równość boków drugie ....współrzędne punktu B spełniają równanie prostej

halohalo: w odpowiedziach B ma byc(2,6),.. a Tobie tu wyszło (4,4)

halohalo: (4,4) to bedzie wysokośc ...robie z róznych równańi B mi nie chce wyjsc

halohalo: zawsze mi wychodzi B(6,2) czemu?

daras: (x_B + 4)² + (y_B + 4)² = 136

	yC − yB
y − yB =		(x − xB) = −(x − xB) podstaw współrzędne A(x,y)
	xC − xB

===: ... źle zrobiłem rysunek To wysokość zawiera się w prostej ... a ja narysowałem, że bok Dobrze Ci wychodzi −

daras: wychodzi (2,6) i (6,2) to są 2 punkty leżące na prostej zawierającej bok ABsymetrycznie względem punktu A