zespolone start
Lukas:
Uzasadnij, że liczba i jest rozwiązaniem równania.
z2+1=0
x2+2xyi−y2+1=0
2xy=0
x2−y2+1=0
x=0 y=0
y2=1 x2=−1 sprzeczność
y=1 lub y=−1
I wyszło, że rozwiązaniem jest i lub −1 ?
Gdzie w takim razie jest błąd ?
21 paź 10:18
Lukas:
2. Uzasadnij równość
Re(z1+z2)=Re(z1)+Re(z2)
Re(x1+yi1+x2+yi2)⇔Re(x1+yi1)+Re(x2+yi2)⇔
x1+x2=x1+x2
?
21 paź 10:22
Lukas:
3. Uzasadnij równość
Im(z1+z2)=Im(z1)+Im(z2)
Im(x1+yi1+x2+yi2)=Im(x1+yi1)+Im(x2+yi2)
(y1+y2)i=(y1+y2)i
?
21 paź 10:25
J :
1) z2 + 1 = 0 ..... z = i ⇔ i2 + 1 = 0 ⇔ −1 + 1 = 0
21 paź 10:28
Lukas:
@J a mogę zapytać czemu rozwiązanie 10:18 jest błędne ?
skorzystałem przecież z definicji z=(x+yi) ?
21 paź 10:29
MQ: Nie i lub −1, tylko i oraz −i.
A poza tym, jaki błąd? przecież wyszło ci, że jednym z rozwiązań jest i.
21 paź 10:30
MQ: @10:22
Raczej tak:
1: Re(z1+z2)=Re(x1+iy1+x2+iy2)=Re((x1+x2)+i(y1+y2))=x1+x2
2: Re(z1)+Re(z2)=Re(x1+iy1)+Re(x2+iy2)=x1+x2
1:=2: ⇒ Re(z1+z2)=Re(z1)+Re(z2)
21 paź 10:35
Lukas:
Dziękuję.
21 paź 10:36
Lukas:
3. Znajdź wszystkie liczby zespolone spełniające podane warunki
z2+4i=0
x2+2xyi−y2+4i=0
(x−y)(x+y)=0
xy=−2
z1=−√2+√2i lub z2=√2−√2i
21 paź 10:42
Lukas:
to samo polecenie
Rez−3Imz=2
Re(x+yi)−3Im(x+yi)=2
x−3y=2
Wszystkie punkty lezące na tej prostej ?
21 paź 10:45
J :
..tak.
21 paź 10:50
Lukas:
@ J będziesz jeszcze na forum po południu ?
21 paź 10:57
J :
... trudno powiedzieć ...

21 paź 10:58
Lukas:

jak to rozpisać ?
21 paź 15:27
J :
z + 1 = x + yi + 1 = (x+1) + yi ... sprzężenie: x+1 − yi
21 paź 15:31
Lukas:
Ok
21 paź 15:37
Lukas:
Na płaszczyźnie zespolonej zaznacz
a) |z+1|=3 ?
21 paź 15:42
J :
Iz + 1I = 3 = I z − (−1) I = 3 ... okrąg o środku w punkcie zo = −1 i promieniu r = 3
21 paź 15:48
Lukas:
ale to −1 na osi urojonej czy rzeczywistej ?
21 paź 15:49
J :
..rzeczywistej...
21 paź 15:50
J :
.. −1 = −1 + 0i
21 paź 15:51
Lukas:
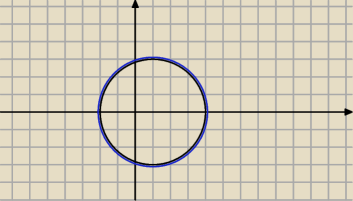
21 paź 16:04
Lukas:
|iz+3|≤2
|(−y+3)+xi|≤2
?
21 paź 16:10
Kacper:
Do tej pory ok.
21 paź 16:12
Lukas:
Ale co dalej zrobić ?
Bo się troszkę pogubiłem.
21 paź 16:18
Mila:
Zadanie) ( 1) Nie miałes polecenia rozwiąż równanie lecz sprawdź,..
spr.
L=z2+1=(i)2+1=−1+1=0 =P
Koniec.
Oczywiście równanie ma dwa rozwiązania
Obliczyłeś y=1 lub y=−1
to masz rozwiązania :
(0+1i)=i oraz (0−1i)=−i
Piszę, bo nie wiem , czy to już dobrze rozumiesz.
Zadanie ostatnie z 16:10, możesz tak.
|iz+3|≤2
|iz−3*i*2|≤2
|i*(z−3i)|≤2
|i|*|z−3i|≤2⇔
|z−3i|≤2 to jest koło o środku (0,3) i r=2
21 paź 17:25
Lukas:
Właśnie nie wiem jak to jest z tymi zespolonymi, za co podstawić żeby sprawdzić czy jest
pierwiastkiem.
21 paź 17:37
Kacper:
Za liczbę z.
21 paź 17:38
Lukas:
|z2+1|=|z+1|
a to jak przedstawić ?
21 paź 17:46
Lukas:
|z2+1|=|z−(−1)| ?
21 paź 17:51
Lukas: ?
21 paź 18:08
Lukas: ?
21 paź 19:38
Lukas: ?
21 paź 20:01
Mila:
A jakie masz polecenie do równania
|z2+1|=|z+1| ?
21 paź 20:05
J :
....a nie masz przypadkiem: Iz2+1I = Iz + iI ...?
21 paź 20:06
Lukas:
zaznacz na płaszczyźnie zespolonej
|z2+1|=|z+i|
21 paź 20:12
J :
.. czyli miałem rację ...

Iz
2+1I = Iz+ iI ⇔ Iz+iI*Iz− 1I = Iz +i I ⇔ Iz − 1I = 1 .... i teraz już poradzisz
sobie...
21 paź 20:16
Kris: |z2+1| = I z + i I*I z− i I
21 paź 20:21
J :
...rysunek post 16:04 ... zły , środek okregu w punkcie (−1,0) , a nie (1,0)..
21 paź 20:27
Mila:
|z2+1|=|z+i|⇔
|z2−i2|=|z+i|⇔
|z−i|*|z+i|=|z+i|⇔
|z−i|*|z+i|−|z+i|=0
|z+i|=0 lub |z−i|=1⇔
z=−i lub |z−i|=1 i co to będzie?
21 paź 20:29
Lukas: okrąg ?
21 paź 20:37
52: Strzelasz czy wiesz? Jak nie wiesz to się pytaj. Ogólnie na jakiej jesteś uczelni Lukas ?
21 paź 20:38
Lukas:
A to ważne na jakie uczelni ?
Wiem, ale wolę się upewnić.
21 paź 20:40
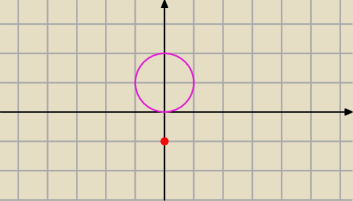
52: Są dwa rozwiązania... to co dwa okręgi ?
21 paź 20:40
52: A się spytałem tylko z ciekawości. Jeśli cię to miało urazić to Przepraszam.
21 paź 20:41
Lukas:
Nie uraziło mnie to ale po prostu nie mam zamiaru tutaj pisać co i gdzie studiuję.
21 paź 20:47
52: Też bym tak narysował

21 paź 20:48
Lukas:
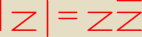
ostatni przykład
21 paź 20:49
Mila:
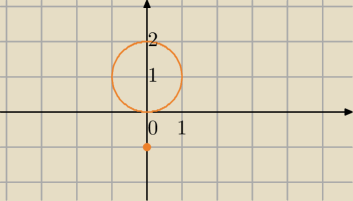
Okrąg , S=(0,1) , r=1 i punkt (0,−1)
21 paź 20:52
Mila:
|z|=z*ź
Tu rozpisz, podstaw:
z=x+iy, x,y ∊R
To ważny przyklad.
21 paź 20:56
Lukas:
|z|=(x+yi)(x−yi)
√x2+y2=x2+xyi−xyi−y2i2
√x2+y2=x2+y2 /2
x2+y2=x4+2x2y2+y4
21 paź 20:59
J :
z*ź = IzI2
21 paź 21:02
Lukas:
|z|=|z|2
√x2+y2=x2+y2 ?
21 paź 21:05
J :
(x+yi)(x−yi) = x2 + y2 = (√x2+y2)2 = IzI2
21 paź 21:05
J :
(x+yi)(x−yi) = x2 + y2 = (√x2+y2)2 = IzI2
21 paź 21:06
Lukas: czyli jak będzie ostatecznie ?
21 paź 21:06
Lukas:
|z|2−|z|=0
|z|(|z|−1)=0
?
21 paź 21:10
Mila:
Właśnie z tego co napisałeś 20:59 wynika to co podał kolega J
Dobrze 21:05 ,21:10⇔
|z|=0 lub |z|=1
Teraz narysuj.
21 paź 21:17
Lukas:
rozpisać z modułu ?
z=0 lub z=1 lub z=−1 ?
21 paź 21:20
52: Mi się wydaje że tak nie wolno...
Po prostu masz pkt(0,0) i okrąg r=1 o środku O(0,0)
Tak myślę.
21 paź 21:24
J :
....nie "i" ... tylko "lub" ... IzI = 0 lub IzI = 1 ...punkt(0,0) lub okrąg S(0,0) r =1
21 paź 21:28
Lukas:
Dziękuję wszystkim za pomoc.
21 paź 21:34
52: J masz rację ... moje przeoczenie.
21 paź 21:41

 jak to rozpisać ?
jak to rozpisać ?

 Iz2+1I = Iz+ iI ⇔ Iz+iI*Iz− 1I = Iz +i I ⇔ Iz − 1I = 1 .... i teraz już poradzisz
sobie...
Iz2+1I = Iz+ iI ⇔ Iz+iI*Iz− 1I = Iz +i I ⇔ Iz − 1I = 1 .... i teraz już poradzisz
sobie...
 Nie uraziło mnie to ale po prostu nie mam zamiaru tutaj pisać co i gdzie studiuję.
Nie uraziło mnie to ale po prostu nie mam zamiaru tutaj pisać co i gdzie studiuję.

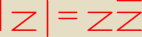 ostatni przykład
ostatni przykład
 Okrąg , S=(0,1) , r=1 i punkt (0,−1)
Okrąg , S=(0,1) , r=1 i punkt (0,−1)