cięciwa habta: Czy łącząc środek cięciwy danego okręgu, z jego środkiem, otrzymamy dwa kąty proste?

PW: Każda prosta zawierająca środek okręgu jest jego osią symetrii.

Kacper: Gdzie dwa kąty proste?

5-latek: A tak trudno zrobic samemu rysunek i zobaczyc czy tak jest ?

habta: 5−latek, rysunek w tym przypadku to żaden dowód... Dzięki PW za sugestię.

PW: Ale nie jest to sugestia "na tak" − cięciwa AB musiałaby w tej symetrii przekształcić się na siebie (wtedy byłyby dwa kąty proste), a tak nie jest zawsze − tylko wtedy, gdy ...

habta: ...cięciwa nie jest średnicą okręgu? ehh.. co ze mnie za matematyk!?

PW: Nie aż tak skrajnie, cięciwa musiałaby być prostopadła do tej prostej łączącej środki, ale wtedy nie ma o co pytać − są dwa kąty proste.

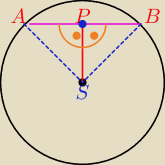
Mila: P− środek cięciwy ΔSPB,ΔSPA− Δprostokątne.

PW: Trochę się drażniłem wczoraj. Po prostu widziałem dowód tak: |SA| = |SB| (są to promienie okręgu) |PA| = |PB| (bo P jest środkiem cięciwy AB). Zbiór punktów jednakowo oddalonych od końca odcinka to symetralna odcinka (jest takie malutkie twierdzenie). Oznacza to, że P i S należą do symetralnej odcinka AB. Wniosek: prosta SP jest symetralną odcinka AB (przez S i P przechodzi tylko jedna prosta), a to oznacza, że kąt między prostymi SP i AB jest kątem prostym. Tak mnie uczyli − jako definicję − że kąt prosty jest to kąt utworzony przez dwie proste, z których jedna jest osią symetrii drugiej.