Monotoniczność ciągów od pewnego miejsca
Ania: zbadać czy podane ciagi są monotoniczne od pewnego miejsca:
a)a(n)=(2n+1)/(n+2)
tu odejmując a(n+1)−a(n) wyszło mi 3(n+3)(n+2), ale nie wiem co dalej robić? Jak sprawdzić
od jakiego miejsca jest monotoniczna?
b) a(n)=1n2−6n+10 i mogę to zrobić sposobem a(n)/a(n+1), czy muszę odejmując
a(n+1)−a(n)? Jęsli tym drugim to poprowiadzicie jakoś? Bo chyba źle zrobiłam bo wynik z
kosmosu mi wyszedł.
20 paź 20:26
===:
a)
zauważ, że w mianowniku masz wielomian kwadratowy ... pierwiastki znasz
Wiesz gdzie przyjmuje on wartości ujemne ... gdzie ma wierzchołek.
Nałóż na to wszystko fakt, że n≥1 .... i wszystko jasne
20 paź 20:41
Ania: czyli mogę napisać że ciąg jest rosnący od −2,5?
20 paź 20:46
===:
b) to może tak:
Zauważ. że mianownik przyjmuje tylko wartości dodatnie (a>0 Δ<0)
wierzchołek dla n=3
Do n=3 mianownik maleje czyli ciąg rośnie a od n=3 rośnie czyli ciąg maleje
20 paź 20:49
===:
a jest wyraz a
−2,5 
? −

20 paź 20:50
Ania: czyli po prostu funkcja jest rosnąca w R?
20 paź 20:56
===:
... przecież mówimy o ciągu

!
Jego wyrazy układają się na wykresie funkcji −

20 paź 20:57
Ania: czyli po prostu f−cja jest rosnąca? ::(
20 paź 20:59
===:
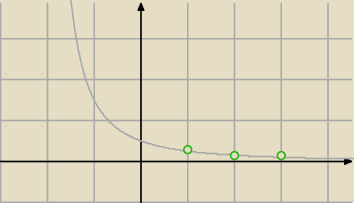
20 paź 21:02
Ania: aaa... dziękuję

20 paź 21:04
===:
−

20 paź 21:10
 ? −
? −
 !
Jego wyrazy układają się na wykresie funkcji −
!
Jego wyrazy układają się na wykresie funkcji −


