13 lis 15:06
;): cos(x−y) jesli tgx=2 siny=−1/2 xnalezy(o;π/2) y nalezy(π,5/2π)
13 lis 15:07
;): tg(π/4+x) gdzie ctgx=2 xnalezy(o.π/2)
13 lis 15:08
;):
13 lis 15:12
Bogdan:
| | 3 | |
czy w pierwszym zadaniu nie powinno być y∊(π, |
| π) ? |
| | 2 | |
13 lis 15:12
;): pierwsze jakos zrobilam
13 lis 15:17
;): chodzi mi o bardziej cos(pi/6+x) gdzie tgx=3/7 x nalezy(pi.3/2 pi)
13 lis 15:18
;): i o tg(π/4+x) gdzie ctgx=2 xnalezy(o.π/2)
13 lis 15:19
;): bogdan racja 3/2
13 lis 15:22
;): jak zrobiles to wyszlo ci cos x=1/5 sinx=2/5 cosy=−5/2
13 lis 15:23
;): moze ktos pomoc:(
13 lis 15:25
Bogdan:
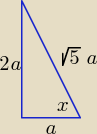
| | π | | 2 | | 1 | |
tgx = 2 i x∊(0, |
| ) ⇒ sinx = |
| i cosx = |
| |
| | 2 | | √5 | | √5 | |
| | 1 | | 3 | | √3 | |
siny = − |
| i y∊(π, |
| π) ⇒ cosy = √ 1 − 1/4 = − |
| |
| | 2 | | 2 | | 2 | |
cos(x − y) = cosx cosy + sinx siny = ...
Czy tak rozwiązałaś pierwsze zadanie ?
13 lis 15:26
;): ok a te nastepne

?
13 lis 15:29
;): tak ale nei moge sobei dac rady z nastepnymi
13 lis 15:30
Bogdan:
W drugim korzystamy z zależności:
| | tgα + tgβ | | ctgβ + ctgα | |
tg(α + β) = |
| = |
| |
| | 1 − tgα tgβ | | ctgα ctgβ − 1 | |
| | π | |
oraz z faktu: ctg |
| = 1 |
| | 4 | |
13 lis 15:32
;): tylko mam pierwiastek 2/5 sin x anie 2/pier/5
13 lis 15:32
;): ale ja mam tg nei ctg
13 lis 15:33
;): w tym tg(π/4+x)...
13 lis 15:33
;): dalej nei wiem jak to zrobic
13 lis 15:34
;): mozesz to rozwiazac bo nei rozumiem

13 lis 15:36
Bogdan:
| | π | |
Wstaw ctgx = 2 oraz ctg |
| = 1 |
| | 4 | |
13 lis 15:45




 ?
?
