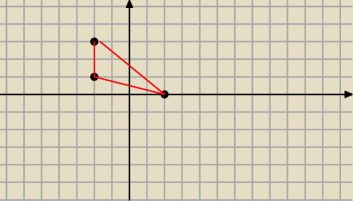
Dany jest trójkąt ABC, gdzie A(-2,3), B(-2,2), C(2,0). Cersei: Dany jest trójkąt ABC, gdzie A(−2,3), B(−2,2), C(2,0). Wyznacz: a) równania ogólne prostych zawierających boki tego trójkąta b) długości wysokości tego trójkąta

J : nie potrafisz napisać równania prostej przechodzącej przez dwa punkty ..?

FizykaTV: a) równanie każdej prostej to ogólnie: y=ax+b boki trójkąta tworzą odcinki AB, BC i CA dla każdego odcinka stwórz układ równań, gdzie pod wzór y=ax+b podstawisz raz współrzędne jednego punktu, a raz drugiego tworzących dany odcinek r−nie prostej AB, A(−2,3) czyli podstawiam x=−2, y=3: zamiast y=ax+b otrzymam: 3=−2a+b B(−2,2) czyli podstawiam x=−2, y=2: zamiast y=ax+b otrzymam: 2=−2a+b układ równań:

⎧	3=−2a+b
⎩	2=−2a+b	układ sprzeczny więc lepiej z rysunku widać, że równanie to x=−2

r−nie prostej BC układ równań:

⎧	2=−2a+b
⎩	0=2a+b	stąd b=1, a=−1/2 a równanie prostej BC to y=−12x+1

r−nie prostej CA układ równań:

⎧	3=−2a+b
⎩	0=2a+b	stąd b=1,5; a=−3/4 a równanie prostej BC to y=−34x+32

b) wyznaczenie wysokości do boku BC: znając równanie boku BC wyznaczasz do niego prostą prostopadłą przechodzącą przez wierzchołek A, a następnie punkt przecięcia prostych. Następnie ze wzoru na odległość między punktami liczysz odległość wyznaczonego punktu od wierzchołka A i tak 3 razy geometrię analityczną tłumaczę w filmiku: https://www.youtube.com/watch?v=UEI8k1FPEqA ============================================= Najlepszy kanał dydaktyczny matma i fizyka http://youtube.com/FizykaTV 89 zadań z fizyki z rozwiązaniami na przykładzie roweru

J : b) ... a po co tak komplikować ... wystarczy wyznaczyć odległość punktu A od pr.BC i cyklicznie...

5-latek: To jest juz z twojej strony lenistwo w czystej postaci Zeby nie zobaczyc w ksiazce jaki jest wzor na rownanie prostej przechodzacej przez dwa punkty Ale co najwazniejsze to zeby nie zrobic rysunku i podac dlugosc wysokosci tego trojkata (sa 3 wysokosci