l.zespolone kyrtap: Korzystając z interpretacji geometrycznej modułu różnicy liczb zespolonych wyznaczyć i naryso− wać zbiory liczb zespolonych spełniających warunki:

	z2+4
I		I≤1
	z−2i

Iz2+4I
	≤1
Iz−2iI

Iz²+4I≤Iz−2iI I(z+2i)(z−2i)I≤Iz−2iI Iz+2iI Iz−2iI ≤ Iz−2iI jak to zinterpretować

J : Po podzieleniu obydwu stron przez Iz−2iI , dostajemy: Iz + 2iI ≤ 1 .... koło S(0,−2) i r = 1.

Hurwitz: Podziel stronami przez |z−2i|≠0. Stąd |z+2i|≤1, to koło o środku w −2i i promieniu 1.

kyrtap: dzięki

kyrtap: zapomniałem o tym założeniu

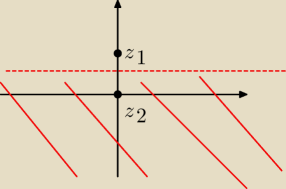
kyrtap: a taki przykład dobrze zrobiłem

	z−3i
I		I> 1
	z

Iz−3iI
	> 1
IzI

Iz− 3iI >IzI

kyrtap:

Godzio : |z| ≠ 0 więc (0,0) wypada z rozwiązania.

J : .... jeżeli przerywana prosta to symetralna odcinka z₁ z₂ .. .to moim zdaniem tak..