l.zespolone
kyrtap: Korzystając z interpretacji geometrycznej modułu różnicy liczb zespolonych wyznaczyć i naryso−
wać zbiory liczb zespolonych spełniających warunki:
Iz + 5iI ≥ I3−4iI
19 paź 20:11
kyrtap: z modułu po prawej stronie mam wyznaczyć promień dobrze myślę?
19 paź 20:15
Hurwitz: Moduł to promień.
19 paź 20:17
kyrtap: czyli będzie IzI =
√32 + (−4)2 =

19 paź 20:18
kyrtap: i potem Iz+5iI ≥5

19 paź 20:18
kyrtap: Dobrze

19 paź 20:22
Hurwitz: Dobrze.
19 paź 20:24
kyrtap: ok dzięki

19 paź 20:25
Hurwitz: A dalej?
19 paź 20:26
kyrtap: już sobie poradzę

bo już przedstawienie geometryczne jest łatwe
19 paź 20:30
kyrtap: czy jeszcze oprócz przedstawienia geometrycznego muszę coś zrobić?
19 paź 20:30
kyrtap: 
19 paź 20:33
Hurwitz: Nie, tylko w tym zadaniu nie chodzi o wyliczenie (tj. z=x+iy itd), tylko o interpretację
modułu.
19 paź 20:36
kyrtap:
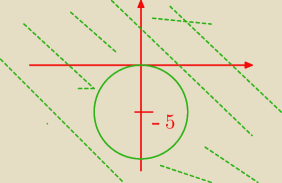
o to chodzi

19 paź 20:41
Hurwitz: Tak, ale jak do tego doszedłeś?
19 paź 20:45
kyrtap: z postaci Iz − (−5i)I ≥5
19 paź 20:47
kyrtap: dobrze?
19 paź 20:54
Hurwitz: ..., że |z−a| mierzy odległość z od a? Czyli my mamy liczby odległe od −5i o niemniej niż 5?
Dobrze.
19 paź 20:55
kyrtap: |z − 1| = |1 + 5i − z| jak mam tutaj w module tą odległość punktów po prawej stronie wyrazić?
19 paź 21:18
Hurwitz: Tu jest zupełnie co innego. |z−1| = |z−(−1−5i)| to zbiór liczb zespolonych, których odległość
od 1 jest taka sama jak od −1−5i. Czyli co to?
19 paź 21:26
kyrtap: odcinek

19 paź 21:35
Godzio :
Taki bardzo długo odcinek

Narysuj sobie dowolne dwa punkty i zacznij zaznaczać punkty równo
odległe od tych dwóch początkowych, zobacz co wyjdzie
19 paź 21:44
kyrtap: nie czaję tego

19 paź 21:52
kyrtap: jak Godzio mógłbyś to zobrazować
19 paź 21:54
Mila:
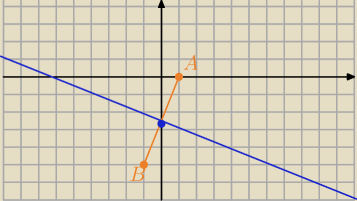
Zbiór wszystkich punktów jednakowo odległych od końców odcinka AB, gdzie
A=(1,0), B=(−1,−5)
19 paź 21:59
kyrtap: dziękuje

ale mam pytanie jak mam narysować taką prostą skoro mam jeden punkt
19 paź 22:00
kyrtap: nie musi to być aż tak dokładnie zobrazowane?
19 paź 22:01
kyrtap: i muszę zapisać sobie SAB jak liczę?
19 paź 22:05
kyrtap: podpowiedzcie mi
19 paź 22:07
Mila:
Przeczytałam równanie H
W Twoim zadaniu, będą inne punkty, zasada ta sama.
19 paź 22:08
kyrtap: no tak wiem wiem ale jak to rysować?
19 paź 22:09
Mila:
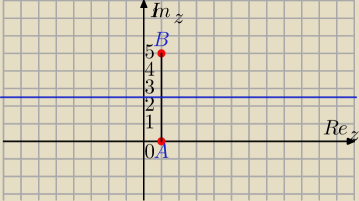
|z−1|=|1+5i−z|
|z−1|=|z−1−5i|⇔
|z−1|=|z−(1+5i)|
zbiór punktów jednakowo odległych od punktów
(1,0) i (1,5) to jest symetralna odcinka.
19 paź 22:16




 bo już przedstawienie geometryczne jest łatwe
bo już przedstawienie geometryczne jest łatwe

 o to chodzi
o to chodzi

 Narysuj sobie dowolne dwa punkty i zacznij zaznaczać punkty równo
odległe od tych dwóch początkowych, zobacz co wyjdzie
Narysuj sobie dowolne dwa punkty i zacznij zaznaczać punkty równo
odległe od tych dwóch początkowych, zobacz co wyjdzie

 Zbiór wszystkich punktów jednakowo odległych od końców odcinka AB, gdzie
A=(1,0), B=(−1,−5)
Zbiór wszystkich punktów jednakowo odległych od końców odcinka AB, gdzie
A=(1,0), B=(−1,−5)
 ale mam pytanie jak mam narysować taką prostą skoro mam jeden punkt
ale mam pytanie jak mam narysować taką prostą skoro mam jeden punkt
 |z−1|=|1+5i−z|
|z−1|=|z−1−5i|⇔
|z−1|=|z−(1+5i)|
zbiór punktów jednakowo odległych od punktów
(1,0) i (1,5) to jest symetralna odcinka.
|z−1|=|1+5i−z|
|z−1|=|z−1−5i|⇔
|z−1|=|z−(1+5i)|
zbiór punktów jednakowo odległych od punktów
(1,0) i (1,5) to jest symetralna odcinka.