granice funkcji Adam555: Wykaż, że prosta k jest asymptotą ukośną wykresu funkcji f:

	2x2+6x−3
f(x)=		k:2x−y+4=0
	x+1

Janek191:

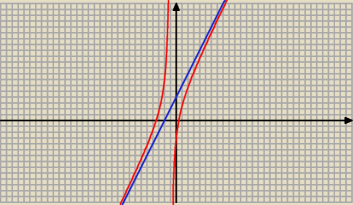
	2 x2 + 6 x − 3
f(x) =		; x ≠ − 1
	x + 1

	f(x)		2 x2 +6x −3		2+6x− 3x2
lim		= lim		= lim		= 2
	x		x2 +x		1+1x

x → +∞ x→ +∞ x→ +∞ m = 2

	2x2 + 6x − 3
lim [ f(x) − m x ] = lim [		− 2x} =
	x + 1

x → +∞ x→ +∞

	2 x2 + 6 x − 3 − 2x*( x + 1)
= lim [		] =
	x + 1

x → +∞

	4 x − 3		4 − 3x
= lim [		] = lim [		] = 4
	x + 1		1 + 1x

x→ + ∞ x→ + ∞ k = 4 Podobnie

	f(x)
lim		= 2
	x

x → −∞ oraz lim [ f(x) − 2 x ] = 4 x → −∞ więc prosta o równaniu y = 2 x + 4 jest asymptotą ukośną danej funkcji

Janek191:

	f(x)
Jeżeli istnieją granice właściwe lim		= m i lim ( f(x) − m x) = k,
	x

x →+∞ x→ +∞

	f(x)
oraz lim		= m i lim ( f(x) − m x) = k
	x

x→ −∞ x → −∞ to prosta y = m x + k jest asymptotą krzywej y = f(x).