zespolone
Radek:
Dla jakich liczb zespolonych zachodzi równość:
Rez2=0
Re(x+yi)2=0
Re(x2+2xyi−y2)=0
x2−y2=0
(x−y)(x+y)=0
x=y lub x=−y
O to chodzi ?
18 paź 22:03
Mila:
Tak.
Np.
z=(2,2)⇔
re(2+2i)2=re(4+4i−4)=re(0+4i)=0
To dla zrozumienia . To nie jest oczywiście dowód.
18 paź 22:11
Radek:
Mogę jeszcze Panią prosić o pomoc ?
18 paź 22:13
Mila:
Pisz.
18 paź 22:29
Radek:
Korzystając z interpretacji geometrycznej modułu różnicy liczb zespolonych narysuj zbiory liczb
zespolonych spełniających podane warunki
a) |z+1|=3
18 paź 22:33
Student : To jest (x+1)2 + y2 = 9
18 paź 22:41
Kris: przypomina coś?
18 paź 22:42
Mila:
To można zapisać tak:
|z−(−1)|=3
Zbió wszystkich punktów , których odległość od punktu(−1,0) jest równa 3⇔
(x+1)2+y2=32 okrąg.
18 paź 22:45
Radek:
Dziękuję.
18 paź 22:47
Radek:
|2iz+6|≤4
2|iz+3|≤4
|xi−y+3|≤2
18 paź 23:00
Mila:
|(3−y)+xi|≤2
√(3−y)2+x2≤2 /
2
x
2+(y−3)
2≤2
2
Wnętrze koła z brzegiem, czyli okręgiem.
II
Można skorzystać z tego ,że i
2=−1 ,|i|=1 i tak:
|2iz+6|≤4⇔
|2iz−6i
2|≤4
2*|i*(z−3i)|≤4
|i|*Iz−3i|≤2
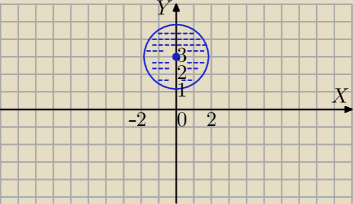
|z−(0+3i)|≤2
wnętrze koła , S=(0,3) i r=2
18 paź 23:21
Radek:
Mam jeszcze jeden
|z+1|+|z−i|=2
18 paź 23:31
Mila:
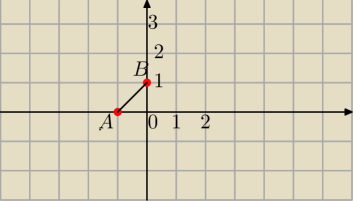
|z+1|+|z−i|=2 ⇔
|z−(−1)|+|z−i|=2 taki zapis oznacza , że suma odległości punktów od punktów :
A(−1,0) i B(0,1) jest równa 2 .
|AB|=
√2<2
to będzie elipsa.
Nie pamiętam wzorów , aby podać osie, może ktoś tu spojrzy to dopisze.
19 paź 00:02
Radek:
a to nie będzie symetralna ?
19 paź 00:03
Mila:
Nie. Powinieneś mieć podane na wykładzie, poczytaj.
Przykład symetralnej:
|z−1|=|z−(1+5i)|
symetralna odcinka AB
A=(1,0) ,B=(1,5)
19 paź 00:09
Radek:
Dobrze doczytam, dziękuję.
19 paź 00:15
 |(3−y)+xi|≤2
√(3−y)2+x2≤2 /2
x2+(y−3)2≤22
Wnętrze koła z brzegiem, czyli okręgiem.
II
Można skorzystać z tego ,że i2=−1 ,|i|=1 i tak:
|2iz+6|≤4⇔
|2iz−6i2|≤4
2*|i*(z−3i)|≤4
|i|*Iz−3i|≤2
|z−(0+3i)|≤2
wnętrze koła , S=(0,3) i r=2
|(3−y)+xi|≤2
√(3−y)2+x2≤2 /2
x2+(y−3)2≤22
Wnętrze koła z brzegiem, czyli okręgiem.
II
Można skorzystać z tego ,że i2=−1 ,|i|=1 i tak:
|2iz+6|≤4⇔
|2iz−6i2|≤4
2*|i*(z−3i)|≤4
|i|*Iz−3i|≤2
|z−(0+3i)|≤2
wnętrze koła , S=(0,3) i r=2
 |z+1|+|z−i|=2 ⇔
|z−(−1)|+|z−i|=2 taki zapis oznacza , że suma odległości punktów od punktów :
A(−1,0) i B(0,1) jest równa 2 .
|AB|=√2<2
to będzie elipsa.
Nie pamiętam wzorów , aby podać osie, może ktoś tu spojrzy to dopisze.
|z+1|+|z−i|=2 ⇔
|z−(−1)|+|z−i|=2 taki zapis oznacza , że suma odległości punktów od punktów :
A(−1,0) i B(0,1) jest równa 2 .
|AB|=√2<2
to będzie elipsa.
Nie pamiętam wzorów , aby podać osie, może ktoś tu spojrzy to dopisze.