funkcja wklęsła
oleńka: Hej możecie pomóc
Wyznaczyć przedziały wklęsłości i wypukłości podanej funkcji f(x) = x4−6x2−6x+1,
Wskazówka. Skorzystać z twierdzenia:
Jeżeli f′′ (x) > 0 dla x należącego do A, to funkcja f (x) jest ściśle wypukła na zbiorze A, a
jeżeli
f′′ (x) < 0 dla x należącego do A, to funkcja f (x) jest wklęsła na zbiorze A.
17 paź 22:41
Saizou :
liczysz 2 razy pochodną i do dzieła
17 paź 22:44
oleńka: a ta druga pochodna to liczę z pochodnej tej pierwszej tak?
17 paź 23:10
5-latek: Powiem CI w zaufaniu ze tak
17 paź 23:29
jakubs: Oleńko, musisz wiesz co to są pochodne wyższych rzędów

17 paź 23:31
Janek191:
f(x) = x
4 − 6 x
2 − 6 x + 1
więc
f '(x) = 4 x
3 − 12 x − 6
oraz
f '' (x) = 12 x
2 − 12 = 12*( x
2 − 1) = 12*( x + 1)*( x − 1)
zatem
f '' (x) > 0 ⇔ ( x + 1)*( x − 1) > 0 ⇔ x ∊ ( −
∞ ; − 1) ∪ ( 1 ; +
∞ )
f'' (x) < 0 ⇔ x ∊ ( − 1; 1)
Odp.
Funkcja f jest wypukła w ( −
∞ ; 1) , ( 1 ; +
∞ )
Funkcja f jest wklęsła w ( − 1; 1).
===========================
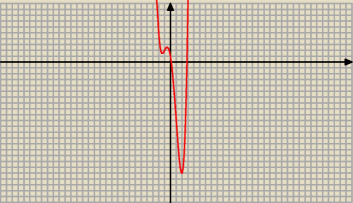
Dodatkowo − wykres danej funkcji
f(−1) = 2 f ( 1) = − 10
18 paź 06:33

 f(x) = x4 − 6 x2 − 6 x + 1
więc
f '(x) = 4 x3 − 12 x − 6
oraz
f '' (x) = 12 x2 − 12 = 12*( x2 − 1) = 12*( x + 1)*( x − 1)
zatem
f '' (x) > 0 ⇔ ( x + 1)*( x − 1) > 0 ⇔ x ∊ ( − ∞ ; − 1) ∪ ( 1 ; + ∞ )
f'' (x) < 0 ⇔ x ∊ ( − 1; 1)
Odp.
Funkcja f jest wypukła w ( − ∞ ; 1) , ( 1 ; + ∞ )
Funkcja f jest wklęsła w ( − 1; 1).
===========================
Dodatkowo − wykres danej funkcji
f(−1) = 2 f ( 1) = − 10
f(x) = x4 − 6 x2 − 6 x + 1
więc
f '(x) = 4 x3 − 12 x − 6
oraz
f '' (x) = 12 x2 − 12 = 12*( x2 − 1) = 12*( x + 1)*( x − 1)
zatem
f '' (x) > 0 ⇔ ( x + 1)*( x − 1) > 0 ⇔ x ∊ ( − ∞ ; − 1) ∪ ( 1 ; + ∞ )
f'' (x) < 0 ⇔ x ∊ ( − 1; 1)
Odp.
Funkcja f jest wypukła w ( − ∞ ; 1) , ( 1 ; + ∞ )
Funkcja f jest wklęsła w ( − 1; 1).
===========================
Dodatkowo − wykres danej funkcji
f(−1) = 2 f ( 1) = − 10