funkcja kwadratowa, parametr Kacperek : Witajcie, nie mam pomysłu jak zrobić takie zadanko: Dana jest funkcja f(x)=|(x−p)² +2p| Dla jakich argumentów równanie f(x)=6 ma dokładnie trzy rozwiązania? Nie chodzi mi o rozwiązanie, tylko o wskazówkę rozwiązania. Pozdrówki

===: ... dla jakich argumentów powiadasz ... a co to jest argument zapytam −

Kacperek : jeju, przepraszam, dla jakich wartości parametrów p*

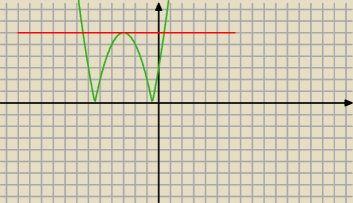
===: ... czy to pomoże? −

Kacperek : Pomogło bardzo, dzięki Jednak czy wyjaśnienie, że f(x)=6 musi przechodzić przez wierzchołek paraboli wystarczy na maturze? W sensie, że pod wartością bezwzględną jest wzór funkcji w postaci kanonicznej, który po wyznaczeniu wartości bezwzględnej będzie przyjmować wykres taki, że jedyną możliwością prostej jest prosta przechodząca przez wierzchołek paraboli (aby miała 3 rozwiązanka). To im wystarczy?

===: albo to ...

===: ... wyjaśnisz, że parabola jest "uśmiechnięta" y_w=−6 czyli 2p=6 p=3

Kacperek : Wiadomo, reszta z wierzchołka paraboli, jednak niedowierzałem, że wystarczy wykresik uproszczony pokazać. Jeszcze raz dzięki

5-latek: === ja tego nie rozumiem Skoro mam taka funkcje f(x)=|(x−p)²+2p| wiem ze to jest postac kanoniczna ale przeksztalce ja do postaci ogolnej |x²−2xp+p²+2p| to jak ja mam ztego narysowac wykres tej funkcji ?

5-latek: ja wiem ze to co bedzie pod osia OX powedruje nad os

5-latek: jesli ma normalne rownanie kwadratowe wmodule to wiem jak taki wykes narysowac

Mila: Z postaci kanonicznej odczytujesz: y_w=2p |2p|=6 2p=6 lub 2p=−6 p=3 lub p=−3 Ponieważ parabola y=(x−p)²+2p jest skierowana do góry , to 2p jest najmniejszą wartością tej funkcji, to jakie wybierasz rozwiązanie?

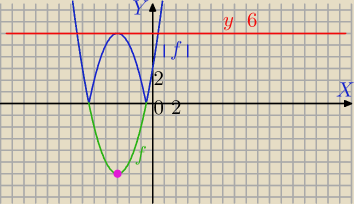
5-latek: Po dlugim namysle wybieram p=−3 (najwyzej bedzie zle ) poniewaz wtedy funkca bez modulu bedzie miala wierzcholek pod osia OX a w module popojdzie nad os OX

Mila:

Mila: Dobrze, kolego. p=−3

5-latek: Ja to pozniej Milu przegyze i napisze jakie ostatecznie rowiazanie wybieram

5-latek: A to tlumaczenie moje 22:35 jest dobre ?

Mila: W porządku, widać, że rozumiesz o co chodzi.

5-latek: Dziekuje Ci Milu Patrzylem teraz tez do ksiazki A. Ehrenfeucht i Stande z 1973r na funkcje kwadratowe i tam nie ma nic na ten temat