Przekształcenia funkcji wymiernej Szczepan: Witajcie, poleceniem zadania jest "Naszkicuj wykres funkcji", ale z tym sobie powinienem poradzić Potrzebuję pomocy w ustaleniu kolejności przekształceń, gdyż sprawia mi to trudności i nie wiem nigdy co jest pierwsze (wartość bezwzględna, czy o wektor). A wiec mam 4 podpunkty:

	x+4
a)f(x)=|		|
	x

	6
b)f(x)=
	|x|−3

	6
c)f(x)=
	|x−2|

	2x−1|x+1|
d)f(x)=
	x−1

Popróbowałem to rozwiązać i mam coś takiego: a)

	x+4		x		4		4		4
f(x)=		=		+		=1+		=		+1
	x		x		x		x		x

	4		4		x+4
f(x)=		→w=[0,1]→		+1→|f(x)|→|		|
	x		x		x

b)

	6		6		6
f(x)=		→w=[3,0]→		→f(|x|)→
	x		x−3		|x|−3

c)

	6		6		6
f(x)=		→f(|x|)→		→
	x		|x|		|x−3|

d) A tutaj nawet nie wiedziałem jak się zabrać Powiedzcie mi czy dobrze to zrobiłem oraz jak zrobić podpunkt d. Byłoby również miło, jakby ktoś wytłumaczył jak robić te przekształcenia (kolejność), bo robiłem to trochę na czuja i poprzez analogię do innego zadania. Szukałem w sieci jak to robić i niestety nie znalazłem.

Szczepan: W mały błąd zrobiłem. Przykład to:

	2x−|x+1|
f(x)=
	x−1

===: d) x≠1 1^o dla x<−1

	2x−(−x−1)		3x+1
otrzymujesz f(x)=		⇒ f(x)=		f(x)=U
	x−1		x−1

===:

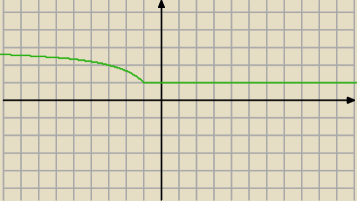
	3(x−1)+4		4
... f(x)=		⇒ f(x)=		+3
	x−1		x−1

2^o dla x≥−1 f(x)=1 stała

Szczepan: A na wykresie trzeba jakoś zaznaczyć kółeczkiem dla x=1, że nie należy, czy niekoniecznie? To już jest jasne, a jak z poprzednimi? Jest jakaś twarda zasada na temat kolejności?

Szczepan: Ponawiam

Szczepan: Nikt nie jest w stanie wytłumaczyć, jak to jest z tymi przekształceniami funkcji + wartość bezwzględna?

===: ... to może napisz czego konkretnie nie rozumiesz. Matematyka to sztuka a nie sztampa −

Szczepan: Nie rozumiem w jakiej kolejności przekształcać funkcje z jednej do drugiej. Tak jak w przykładach a,b,c. Z jakiejś funkcji do jakiejś. Raz jest |f(x)| pierwsze, raz o wektor, a jeszcze innym razem f(|x|). Gorzej jak jeszcze dochodzi odbicie względem jakiejś osi.