Styczne do okręgu przecinające się z prostą l pod kątem x malefica: Napisz równania tych stycznych do okręgu o równaniu x²+2x+y²−3 = 0, które przecinają się z prostą x√3 − y + 1 = 0 pod kątem ^π₃ Wyliczyłem środek okręgu S(−1;0). Wiem też, że istnieje wzór na kąt, pod którym przecięte są proste

	a1 − a2
tgα= |		|
	1+a1*a2

Wyliczyłem a₂=0 ∨ a₂= −√3, jednak nie wiem co dalej.

J : a dlaczego dostałeś/aś dwa rózne wspólczynniki , skoro te proste muszą być równoległe..?

J : ... dana prosta y = √3x + 1 , jest nachylona do osi OX pod kątem 60^o , zatem szukane proste będa nachylone do osi OX pod kątem 60^o +60^o = 120^o , czyli będą to proste: y = −√3 + C i odległe od środka okregu o wartość promienia.

malefica: To są odpowiedzi do tego zadania podane przez profesora: y=−2 y=2 y=−√3+√3+√14 y=−√3+√3−√14 Może chodzi o coś na zasadzie, że prosta z pierwszą prostą utowrzy kąty 30 i 60, a z drugą 60 i 30? Miałem nadzieje, że pomysł na rozwiązanie mi to rozjaśni

malefica: pomyłka, druga para rozw. y=−√3x+√3+√14 y=−√3x+√3−√14

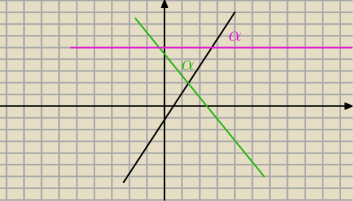
J : ...tak, obie proste tworzą z daną kąt α = 60^o .. a₁ = 0 lub a₂ = −√3

malefica: No tak, ale szczerze mówiąc dalej nie mam pojęcia jak wyznaczyć wzory stycznych Dwie pierwsze odp. można wywnioskować z wykresu, ale pkt stycznej leżącej na okręgu? y=−√3x+b Jak wyliczyć b? Próbowałem wyznaczyć prostopadłą do tej prostej przechodzącej przez S(−1;0)

	1		1
wyszło y=		x+
	√3		√3

1		1
	x+		=−√3x+b /*√3
√3		√3

x+1=−3x+√3b 4x+1=√3b

	4√3		√3
b=		x+
	3		3

nic to nie daje, czy można coś z tym zrobić? Jakieś inne możliwości wyliczenia tych pkt?

malefica: W dodatku styczna o wzorze z odpowiedzi w ogóle nie styka okręgu, który wyliczyłem x²+2x+y²−3 = 0 (x+1)²+(y−0)²=4 S(−1,0) r=2, jest tu jakiś błąd? 0.o