~(p=>q)<=>p^~q
Studentka_9: Ktoś pomoże? Jestem początkująca w tych sprawach...
Logika
~(p=>q)<=>p~q
16 paź 21:23
Kacper:
Tabelka i sprawdzasz.
16 paź 21:23
Hurwitz: "Ktoś pomoże? Jestem początkująca w tych sprawach..."
Czy komuś też skojarzyło się z czymś innym (lecz równie przyjemnym jak matematyka)

?
16 paź 21:27
Studentka_9: Kacper − jaka tabelka?

Hurwitz − wybacz tak to jest z ludźmi po 12 godzinnym maratonie na uczelni z jednym okienkiem
co trwał 1,5 godziny

16 paź 21:31
PW: Hurwitz, dokładnie to samo

16 paź 21:43
Saizou :
sprawdźmy czy jest to tautologia np. metodą skróconą, czyli załóżmy że nie jest to tautologia,
zatem
¬(p→q)↔p∧¬q=0 (kiedy równoważność jest fałszywa?)
[¬(p→q)=1 i p∧¬q=0 ] lub [¬(p→q)=0 i p∧¬q=1]
[p→q=0 i p∧¬q=0] lub [p→q=1 i p∧¬q=1]
[p=1 i q=0 i p∧¬q=0] lub [p→q=1 i p=1 i ¬q=1 ]
1∧1=0 1→0=1
sprzeczność sprzeczność
zatem wyjściowy schemat zdania jest tautologią
16 paź 21:59
Saizou :
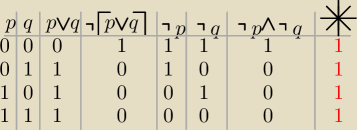
albo tabelką zero−jedynkową
gwiazdka to ¬(p→q)↔p∧¬q
czyli to tautologia
16 paź 22:12
5-latek: Czesc
Saizou 
Pewnie jestes juz bardzo zmeczony ale w 3 i 4 kolumnie ma byc impilikacja a nie
alternatywa
tak w ogole to jest prawo zaprzeczenia implikacji
16 paź 22:18
Saizou :
cześć, a tak się narobiłem nad tabelką

hehe bo nie to przepisałem, bo robiłem sobie dzisiaj przykłady z tego i miałem pod ręką
na wykładach 17) ważniejszych tautologii i je sobie sprawdzałem xd
16 paź 22:21
5-latek: Ale ma juz wzor jak robic .
16 paź 22:26
Saizou : ale metoda skrócona jest chyba dobrze

16 paź 22:27
5-latek: Ale pewnie zobaczy rano bo dzisiaj byla bardzo zmeczona nasza kolezanka

16 paź 22:28
Saizou :
wiesz każdy ma prawo do odpoczynku, ale nie ma to jak łacińskie określenia tautologii np.
tercium non datur, duplex negatio affirmat, reductio ad absurdum
16 paź 22:33
Hurwitz: Gdzieś to już pisałem... Funktory zdaniotwórcze (koniunkcja, alternatywa, zaprzeczenie,
implikacja, itd) mają "tę samą siłę" − żaden nie działa mocniej niż pozostałe (dla działań
mnożenie i dzielenie mają pierwszeństwo przed dodawaniem i odejmowaniem). W konsekwencji zapis
~(p=>q)<=>p~q
należało by czytać "od lewej do prawej" (takie są zasady), tj.
[~(p=>q)<=>p] ~q
a to tautologią nie jest.
16 paź 22:37
Saizou :
A ja na wykładach miałem że
koniunkcja i alternatywa wiążą mocniej niż implikacja i równoważność
16 paź 22:42
5-latek: ja przynajmniej patrzylem na to co napisala na gorze postu nie potem .
16 paź 22:43
Hurwitz: A, jak implikację i równoważność zapiszesz jako koniunkcję i alternatywę? To jak wtedy pójdzie?
Od lewej do prawej czy jednak jakiś nawias się pojawi?

16 paź 22:48
Saizou :
dodam potrzebne nawiasy

dlatego wolę symbolikę bez nawiasową Łukasiewicza
16 paź 22:51
Hurwitz: Nie chcę mieszać... Kiedyś takie złośliwe zadanie widziałem, gdzie trudność polegała na tym, że
nie bardzo wiadomo było w jakiej kolejności co sprawdzać...
16 paź 22:52
Saizou :
dlatego jest lepsza symbolika bez nawiasowa

16 paź 22:54
Janek191:
@Saizou:
Beznawiasowa symbolika Łukasiewicza !

18 paź 07:10
Janek191:
∼ ( p ⇒ q ) ⇔ p ∧ ∼ q
Można też skorzystać z prawa : ( p ⇒ q ) ⇔ ( ∼ p ∨ q )
Mamy
( p ⇒ q ) ⇔ ( ∼ p ∨ q )
Zaprzeczamy obustronnie
∼ ( p ⇒ q ) ⇔ ∼ ( ∼ p ∨ q ) ⇔ ∼ ( ∼ p) ∧ ( ∼ q ) ⇔ p ∧ ∼q
18 paź 07:24
 ?
?
 Hurwitz − wybacz tak to jest z ludźmi po 12 godzinnym maratonie na uczelni z jednym okienkiem
co trwał 1,5 godziny
Hurwitz − wybacz tak to jest z ludźmi po 12 godzinnym maratonie na uczelni z jednym okienkiem
co trwał 1,5 godziny 

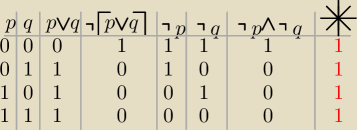 albo tabelką zero−jedynkową
gwiazdka to ¬(p→q)↔p∧¬q
czyli to tautologia
albo tabelką zero−jedynkową
gwiazdka to ¬(p→q)↔p∧¬q
czyli to tautologia
 Pewnie jestes juz bardzo zmeczony ale w 3 i 4 kolumnie ma byc impilikacja a nie
alternatywa
tak w ogole to jest prawo zaprzeczenia implikacji
Pewnie jestes juz bardzo zmeczony ale w 3 i 4 kolumnie ma byc impilikacja a nie
alternatywa
tak w ogole to jest prawo zaprzeczenia implikacji
 hehe bo nie to przepisałem, bo robiłem sobie dzisiaj przykłady z tego i miałem pod ręką
na wykładach 17) ważniejszych tautologii i je sobie sprawdzałem xd
hehe bo nie to przepisałem, bo robiłem sobie dzisiaj przykłady z tego i miałem pod ręką
na wykładach 17) ważniejszych tautologii i je sobie sprawdzałem xd



 dlatego wolę symbolikę bez nawiasową Łukasiewicza
dlatego wolę symbolikę bez nawiasową Łukasiewicza

