W czworokącie wypukłym kolejne boki mają długości Problematyczny: W czworokącie wypukłym kolejne boki mają długości równe: 2cm, 5cm, 7cm i 2√13cm. Jedna z przekątnych ma długość 8cm. Oblicz długość drugiej przekątnej tego czworokąta z dokładnością do 0,1. Prosiłbym o rozwiązanie oraz takie szybkie wytłumaczenie.

wmboczek: pewnie pomyliłem się w rachunkach ale na oko √39 policz pola trójkątów o danych bokach z 8 wyznacz wysokości opuszczone na 8 zauważ, że 8 dzieli kąt między 2 i 5 na 2 kąty po 60 stopni każdy z tw. cosinusów policz wynik

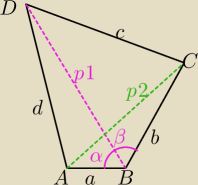
Domel: a = 2cm; b = 5cm; c = 7cm; d = 2√13 = ~7,2111cm 1° przekątna p1 o dł. 8cm może być tylko z narożnika "B" do narożnika "D" bo tylko suma a+d jest większa od 8cm − czyli łuk o dł. 8cm z narożnika B przetnie się z łukiem o dł 2√13 z narożnika A w punkcie D. A łuk o dł. 8cm z narożnika A i łuk o dł. 5cm z narożnika B nie przetną się bo a+b < 8cm − czyli mielibyśmy koło w kole i nie powstałby punkt C Is clear 2° Z twierdzenia cosinusów (https://matematykaszkolna.pl/strona/543.html) możesz wyliczyć kąty α i β.

	a2 + p12 − d2		π
Np d2 = a2 + p12 − 2*a*p1*cosα => cosα =		= 0,5 => α =
	2*a*p1		3

Kąt β wylicz sam 3° Jeżeli masz kąty α i β oraz długości a i b to możesz z tw. cosinusów policzyć p2 DO BOJU i Good luck