Parametr terry: Dla jakich wartości parametru a równianie |x − 1| = a² − 4a − 1 ma dwa pierwiastki dodatnie? 1. W odpowiedziach jest, że mogę to zacząć tak: rysuję wykres funkcji f(x) = |x − 1| i mam, że dla przedziału (0, 1) funkcja ma 2 pierwiastki dodatnie. Że niby co? Przecież f(x) = |x − 1| ma tylko jeden pierwiastek: x = 1. Wyjaśni ktoś o co chodzi? 2. Mógłby ktoś ogólnie wytłumaczyć bardziej łopatologicznie co mam tutaj zrobić w tym zadaniu? Bo niezbyt rozumiem polecenie.

ZKS: Dla przedziału (0 ; 1) tak, więc 0 < a² − 4a − 1 < 1.

bezendu: Zadania z kiełbasy ? ZKS mi to tłumaczył zaraz poszukam linku.

bezendu: https://matematykaszkolna.pl/forum/159314.html

PW: Wykres funkcji f(x) = |x−1| to taki "dzióbek"1 stojący w punkcie x₀ = 1.Narysuj jak radzą i przetnij go prostą y=u, u >0. Co otrzymasz w punktach przecięcia?

PW: Mateńko, w tym 159314 jest taka dyskusja, że zawrót głowy. Może odpowiedz na pytanie z 20:39 .

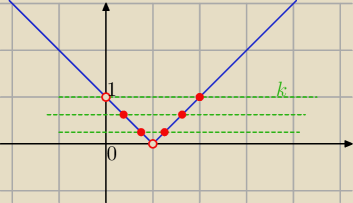Eta: f(x)=|x−1| −−− wykres y= k −−−proste równoległe do osi OX przecinają wykres f(x) w dwu punktach po prawej stronie osi OX ( bo mają być dwa pierwiastki dodatnie dla k∊(0,1) ⇒ a²−4a−1>0 i a²−4a−1<1 rozwiąż układ tych nierówności i jako odp podaj część wspólną rozwiązań tych nierówności

terry: OK, dzięki. Tylko zgłupiałem − dlaczego te pierwiastki to wartości z osi igreków? Zawsze myślałem, że pierwiastek to miejsce zerowe...

PW: I dobrze myślisz. Punkty przecięcia pokazują, że wartości są jednakowe − to na osi igreków (przecież ma być spełnione równanie), a na osi iksów − dla jakich x te wartości są równe. Rozwiązania równości są na osi iksów. Teraz tylko trzeba sobie uzmysłowić, że za wysoko z tym "k" z rysunku Ety nie podskoczysz, bo rozwiązania (właśnie te iksy) zaczynają być różnych znaków, a miały być oba dodatnie.